Department of Mathematics --- College of Science --- University of Utah

Mathematics 1010 online

Worked Word Problems

This page contains a number of worked word problems. Of course, no list could be complete, but there are certain pattern that occur over and over.

  1. Percent, unknown base amount. After a 10 percent raise your hourly wage is $ \char36 10.- $. How much did you make before?

    Solution: Let's say your previous wage was $ x $ dollars per hour. You are now making 10 percent more. In other words, you are making $ 110 $% of your old wage. Hence

    $\displaystyle 10 = 1.1 x $

    which means

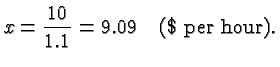
    $\displaystyle x = \frac{10}{1.1} = 9.09 \quad\hbox{(\char36~ per hour)}. $

  2. Percent, unknown discount and tax. You buy a pair of pants whose listed price is $ \char36 40.- $. There is a sale, and the dealer offers a discount of $ 30 $%. However, you also have to pay $ 10 $% sales tax. What do you pay in total?

    Solution: The discount applies to the list price of $ \char36 40.- $. The sales tax applies to the discounted price. $ 30 $% of $ \char36 40.- $ is $ 0.3\times \char36 40 = \char36 12.- $. The discounted price therefore is $ \char36 40 - \char36 12 = \char36 28. $ (Equivalently you could argue that you buy the pants for $ 70 $% of the list price, which is $ 0.7 \times \char36 40 = \char36 28.- $) You still need to pay $ 10 $% sales tax on the price of $ \char36 28.- $. Since $ 10 $% percent of $ 28 $ is $ 2.8 $ your total price is

    $\displaystyle \char36 28 + \char36 2.8 = \char36 30.80. $

  3. Percent, unknown percentage. Ten years ago, the population of your town was $ 100,000 $. Now it is $ 180,000 $. What is the average annual growth rate?

    Solution: Let's call the growth rate $ p $. Every year the population gets multiplied with $ \frac{p}{100} $. The problem tells us that

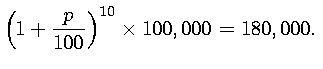
    $\displaystyle \left(1+\frac{p}{100}\right)^10 \times 100,000 = 180,000. $

    Dividing by $ 100,000 $ on both sides gives

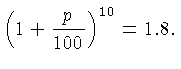
    $\displaystyle \left(1+\frac{p}{100}\right)^10 = 1.8. $

    To get rid of the exponent $ 10 $ we take both sides to the power $ \frac{1}{10} $. (See the pages on powers and roots and radicals. ) This gives

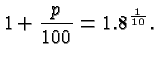
    $\displaystyle 1+\frac{p}{100} = 1.8^{\frac{1}{10}}. $

    Subtracting $ 1 $ on both sides, and then multiplying with $ 100 $ gives

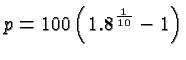
    $\displaystyle p = 100\left(1.8^{\frac{1}{10}}-1\right) $

    This expression can be evaluated with a calculator, and works out to approximately $ 6.05 $%.

  4. Mixture Problems. Suppose you mix a gallon of 5% vinegar with two gallons of 20%vinegar. What's the percentage of vinegar in the resulting mixture?

    Solution: The main difficulty here is to understand the meaning of the phrase 5% vinegar. Think of ordinary vinegar as a mixture of water and pure (100%) vinegar. 5% vinegar means that the ratio of the pure vinegar in the mixture, and the total amount of fluid is 0.05 (or 5%). In this example the total amount of the fluid is 3 gallons, and the total amount of pure vinegar is $ 0.05+2\times 0.2 $ gallons (i.e., 5% of the 1 gallon and 20% of the two gallons). The ratio of pure vinegar to total amount of fluid is, therefore,

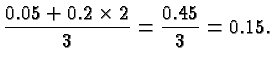
    $\displaystyle \frac{0.05 + 0.2 \times 2}{3} = \frac{0.45}{3} = 0.15. $

    The result is 15% vinegar. In variations of this problem other ingredients may be unknown (like the amount you add to get a mixture of a specified strength.) In that case use a variable for the unknown, and solve the resulting equation.

  5. Work Rate Problems. You can paint a room in 2 hours, and your brother can do the same in 3 hours. How long does it take the two of you working together?

    Solution: The trick for this kind of problem is to think of the job as the basic unit. You want to do 1 job, i.e., paint that room. You can do 1/2 of that job in one hour, and your brother can do 1/3 of the job in one hour. Painting together the two of you will do $ \frac{x}{2} + \frac{x}{3} $ of that job in $ x $ hours. Thus we need to solve the equation

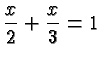
    $\displaystyle \frac{x}{2}+\frac{x}{3} = 1 $

    which gives

    $\displaystyle x=\frac{6}{5}\hbox{~hours} = 70\hbox{~minutes}. $

    There are variations of this. depending on what is known, but in all cases think of the job as your basic object.

  6. Pythagorean Theorem Problems. Your laser range meter tells you that the distance to the top of a nearby mountain is 3 miles. Your map tells you that the horizontal distance from you to (a point underneath) the top of that mountain is 2.8 miles. How tall is the mountain?

    Solution: The solution to all such problems proceeds by drawing a picture, and then applying the Pythagorean Theorem. In this case we get the following Figure which shows the mountain in a fetching green color:

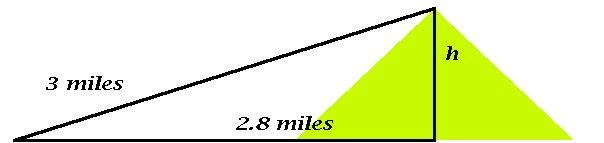
    Denoting the unknown height by $ h $ we get the equation

    $\displaystyle h^2+2.8^2=3^2. $

    Subtracting $ 2.8^2 $ and taking the square root on both sides gives

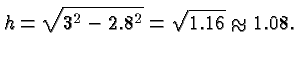
    $\displaystyle h = \sqrt{3^2-2.8^2} = \sqrt{1.16} \approx 1.08. $

    That mountain is a little over a mile high (like some of the mountains near Salt Lake City).

  7. Scaling Problems You cover the replica of a famous statue of Archimedes with gold leaf, and you pay $200 for the gold. You like the statue so much that your spouse acquires the original, and gives it to you for your birthday. The original is just like the replica, except it's 3 times as tall, wide, and deep. Both the replica and the original are made of solid marble. You cover the original statue with gold leaf also. How much do you pay for the required gold? Your replica weighs 2 tons. How much does the original statue weigh?

    Solution: There are quite a few problems like this in the homework sets because they provide excellent exercises in applying radicals. As pointed out on the scaling page, multiplying each linear dimension with a factor multiplies every area with the square of that factor, and the volume (and weight) with the cube of that factor. Everything flows from that basic fact! In this case we multiply linear dimensions with 3, and so we multiply the area (and hence the price of the gold leaf) with $ 3^2=9 $ and the volume (and hence the weight) of the statue with $ 3^3=27 $. You pay $1,800 for the gold leaf, and your original statue weights 54 tons.

    You now begin to wonder how much it will cost to reinforce your floor, or whether you should perhaps remove the floor altogether and place your statue in the basement. But it is a beautiful statue!

    In some of the homework problems in this course you are given (explicitly or implicitly) a factor that multiplies the area or the volume. As explained on the scaling page, if you multiply the areas with $ r $ you multiply the lengths with $ \sqrt{r} $ and the volume with $ r^{\frac{3}{2}} $, and if you multiply the volume with $ r $ you multiply the lengths with $ r^{\frac{1}{3}} $ and the areas with $ r^{\frac{2}{3}} $.

  8. Throwing Rocks.

    You throw a rock and release it at a height of $ 6 $ feet. Its initial vertical velocity is $ 20 $ feet per second (going up) and its horizontal (forward) velocity is $ 25 $ feet per second. How far does the rock fly until it hits the ground, and what is the maximum height that it reaches?

    Solution: According to the discussion of throwing rocks the height of the rock at the time $ t $ is given in general by $ h(t) = -\frac{1}{2}gt^2+v_0t+h_0. $ In our case $ g=32 $ feet per second squared (since we are on earth), $ v_0 = 20 $ feet per second (the initial upward motion), and $ h_0=6 $ feet, the height at which we release the rock. The height of the rock at time $ t $, therefore, is given by $ h(t) = -16t^2+20 t+6. $ To find out at what time the rock hits the ground (where the height is zero) we need to solve the quadratic equation $ -16t^2+20 t+6 = 0 $ which gives $ t=1.5 $ seconds as the time of impact. During that time the rock covers a distance that's obtained by multiplying the flight time with the horizontal velocity, which gives the distance $ d=1.5\times25 = 37.5 $ feet. At the time that the rock reaches its maximum height its vertical velocity, which in general is given by $ v(t) = -32t+v_0, $ is zero. In our case $ v_0 = 20 $ and hence the time $ t_h $ at which the rock reaches the maximum height is given by $ t_h = \frac{20}{32} = 0.625 $ seconds. At that time the rock is a height $ h_{\max} = h(t_h) = 12.25 $ feet.