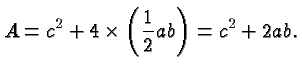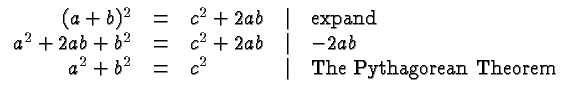Department of Mathematics --- College of Science --- University of Utah

Mathematics 1010 online

The Pythagorean Theorem

Some of the homework problems in this class require the Pythagorean Theorem, named after Pythagoras who lived approximately 380-300 BC. That Theorem is also used for example when computing the distance between two points in the Cartesian Coordinate System.

The Pythagorean Theorem states that in a right triangle the squares of the two short sides add to the square of the long side. If we call the lengths of the two short sides $ a $ and $ b $, and the length of the long side $ c $ this leads to the familiar statement

$\displaystyle c^2 = a^2 + b^2.\qquad\qquad(*) $

Of course, the sides need not be called $ a $, $ b $ and $ c $, and the reverse of the above statement also holds: if the equation $ (*) $ holds than the triangle in question is a right triangle.


The Pythagorean Theorem

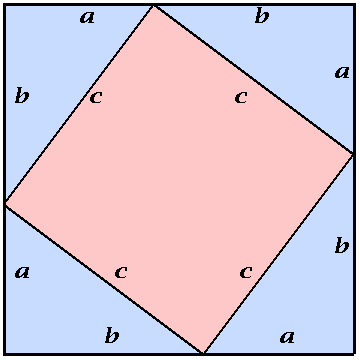
The Figure on this page illustrates a simple proof of the Pythagorean Theorem. We describe that proof here because it provides a beautiful application of Intermediate Algebra. Take four right triangles (shown in blue) with sides $ a $, $ b $ and $ c $ and line them up as indicated in the Figure. Thus we continue the side $ a $ of one triangle with the side $ b $ of another. The result is a square whose sides have length $ a+b $. It encloses a smaller square (shown in red) whose sides have length $ c $.

Let

$\displaystyle A=(a+b)^2 $

denote the area of the large square. It can also be computed by adding the areas of the four triangles and the area of the inner square. The area of one blue triangle equals $ \frac{1}{2}ab $ (which is half of base times height). Thus we also have

$\displaystyle A = c^2 + 4 \times \left(\frac{1}{2}ab\right) = c^2 + 2ab. $

The two expressions are equal and we obtain:

$\displaystyle \begin{array}{rclcl} (a+b)^2 &=& c^2 + 2ab &\vert& \hbox{expand} ... ... 2ab \\ a^2+b^2 &=& c^2 &\vert& \hbox{The Pythagorean Theorem}\\ \end{array} $