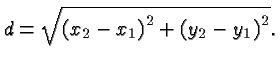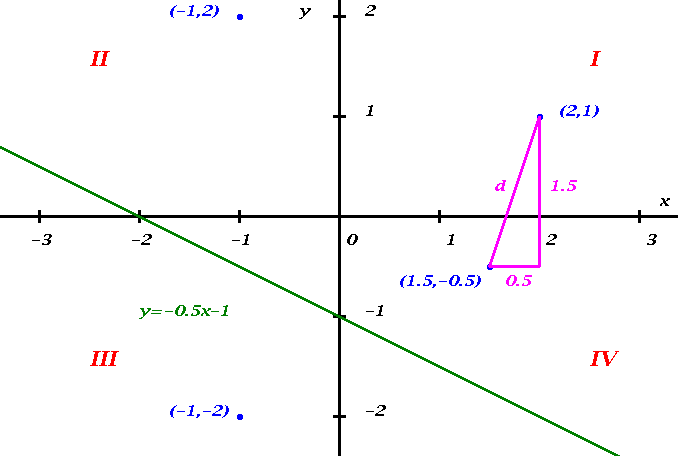
You are actually familiar with Cartesian Coordinates, they are used to express addresses in Salt Lake City. The Cartesian Coordinate System (also called Rectangular Coordinate System ) is named after its inventor Renee Descartes (1596-1650). It greatly amplifies our problem solving ability by letting us think about algebraic problems geometrically, and about geometric problems algebraically.
Consider the Figure above. The Cartesian Coordinate System consists of a
vertical and a horizontal number line that intersect perpendicularly
at their origins.
The intersection is also called the origin of the coordinate system.
The number lines are called the axes of the system.
The word axes is the plural of the word axis.
Thus there is a
horizontal axis, and a vertical axis. The variable along the
horizontal axes is commonly called
The location of a point can be described by two numbers that are
obtained by projecting the point perpendicularly onto each of the
coordinate axes. The projection onto the horizontal axis is the
Conversely, given two numbers, one being the
Obviously one can draw only a finite part of the infinite
coordinate system. Which part to draw depends on the problem at hand.
In a certain context your figure may or may not contain the origin, and
it may have different scales along the two axes.
The two coordinate axes divide the plane into four parts. These
are called quadrants, and they are numbered I, II, III, IV, starting
with the Northeast quadrant and moving counterclockwise. The
quadrants are indicated in red in the above Figure.
We talk about the first, second, etc., quadrant.
Of major importance is the concept of the graph of an equation.
Given an equation involving the two variables
The Figure on this page contains the graph of the equation
The graph of that equation is a straight line extending to
infinity in both directions. In this class, we will study equations defining
straight lines in great detail.
If the scales on the vertical and horizontal axes are the same then
the distance
between two points is just what you would measure with a ruler. This fact is
illustrated in the above Figure by the magenta triangle. Let
Drawing a similar picture involving two general points
![]() , and that along the vertical axis is
called
, and that along the vertical axis is
called ![]() . Other choices are possible, but we will use this particular
choice almost universally in this class. Accordingly the horizontal
axis is also called the
. Other choices are possible, but we will use this particular
choice almost universally in this class. Accordingly the horizontal
axis is also called the ![]() -axis, and the vertical axis the
-axis, and the vertical axis the
![]() -axis. Collectively the axes are also called the coordinate
axes. By convention the horizontal axis points to the right, and the
vertical axis points up.
-axis. Collectively the axes are also called the coordinate
axes. By convention the horizontal axis points to the right, and the
vertical axis points up.
Coordinates
![]() -coordinate, and the projection onto the vertical axis the
-coordinate, and the projection onto the vertical axis the
![]() -coordinate. A point is described by the two coordinates,
separated by a comma and enclosed by parentheses, with the
-coordinate. A point is described by the two coordinates,
separated by a comma and enclosed by parentheses, with the
![]() -coordinate coming first. The Figure above shows four points
--specifically the points
-coordinate coming first. The Figure above shows four points
--specifically the points ![]() ,
, ![]() ,
, ![]() , and
, and
![]() --
and their representation as pairs of numbers, all drawn in blue.
--
and their representation as pairs of numbers, all drawn in blue.
![]() -coordinate and
the other the
-coordinate and
the other the ![]() -coordinate, there is a unique point in the
Cartesian Coordinates System that corresponds to that pair of numbers.
-coordinate, there is a unique point in the
Cartesian Coordinates System that corresponds to that pair of numbers.
Quadrants
![]() and
and ![]() , the
graph of an equation is the set of all points
, the
graph of an equation is the set of all points ![]() whose
coordinates satisfy the equation.
whose
coordinates satisfy the equation.
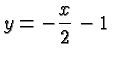
The Distance between Two Points
![]() be
the distance between the points
be
the distance between the points ![]() and
and ![]() . The
horizontal side of the triangle has a length of
. The
horizontal side of the triangle has a length of ![]() , and the
vertical side a length of
, and the
vertical side a length of ![]() . By the
Pythagorean Theorem,
. By the
Pythagorean Theorem,
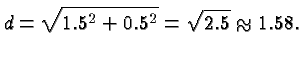
![]() and
and ![]() you can see that the
distance between these two points is
you can see that the
distance between these two points is