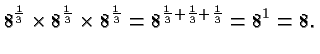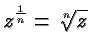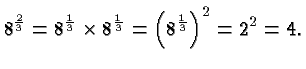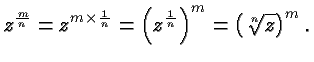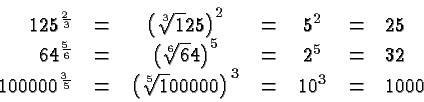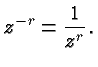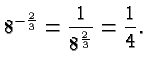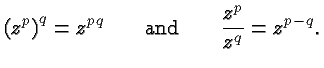Powers
Powers provide a beautiful and compact illustration of two major
principles in mathematics:
-
Introduce concepts in a simple context and then
generalize them in such a way that rules and facts that are true in
the simple context remain true in the more general context.
-
Reduce your problem to one you have solved
before.
In this way we obtain powerful problem solving tools, and we
deepen our understanding of mathematics.
Multiplication
We start by observing that multiplication is defined by repeated
addition.
Thus for any number 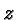 ,
More generally, for any number
,
More generally, for any number 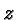 and any
natural number
and any
natural number 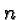 (i.e., one of
(i.e., one of
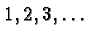 ) we define
the product
We then extend this definition to factors
) we define
the product
We then extend this definition to factors 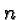 that are not natural
numbers
(like fractions, negative numbers, or, in general, real numbers) in
such a way that the ordinary rules of arithmetic remain true.
that are not natural
numbers
(like fractions, negative numbers, or, in general, real numbers) in
such a way that the ordinary rules of arithmetic remain true.
Natural Number Exponents
Powers work exactly the same way, except that instead of addition
we use multiplication as our basic repeated operations. Thus we
define, for any number 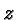 and any natural number
and any natural number 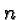 ,
For example,
The expression
,
For example,
The expression 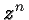 is called a power and described in words as
is called a power and described in words as
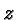 to the power
to the power 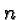 . The number
. The number 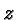 is the base of the power,
and the number
is the base of the power,
and the number 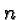 is its exponent .
Just like anybody should know the multiplication table it is
useful to know some basic powers by heart, like those given in the
following table:
Note that our definition of a power only applies when the exponent is a
natural number. The base, however,
can be any real number. Our task now is to extend this definition to
exponents that are more general than natural numbers. We want to do
this in a useful way, which means that all the rules that apply for
natural number exponents also apply for more general exponents.
is its exponent .
Just like anybody should know the multiplication table it is
useful to know some basic powers by heart, like those given in the
following table:
Note that our definition of a power only applies when the exponent is a
natural number. The base, however,
can be any real number. Our task now is to extend this definition to
exponents that are more general than natural numbers. We want to do
this in a useful way, which means that all the rules that apply for
natural number exponents also apply for more general exponents.
The Central Rule
So what are those rules? Consider, for example the product
In general it is true that (for any real
number 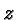 and natural numbers
and natural numbers 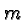 and
and 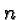 ):
We'll call this fact our central rule. It follows straight
from the definition: we write down
):
We'll call this fact our central rule. It follows straight
from the definition: we write down 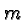 factors
factors 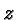 , and then
, and then 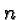 factors
factors 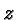 , and so we write down a total of
, and so we write down a total of 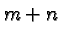 factors
factors 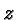 .
.
Zero Exponents
Now consider the case where the exponent is zero. Read this
paragraph carefully. It is elementary and understandable, and yet it
illustrates a wide swath of mathematical thinking. We want our central
rule to apply. For example we want to have
So 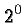 is a number that gives
is a number that gives 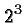 when multiplied
with
when multiplied
with 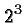 . There is only one such number, namely the number
. There is only one such number, namely the number 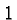 .
So we are compelled to define
.
So we are compelled to define 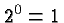 . If a base was a number
other than
. If a base was a number
other than 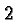 , say
, say 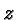 , the same sort of argument applies, and so
we define
, the same sort of argument applies, and so
we define 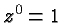 . There is one caveat, however. If
. There is one caveat, however. If 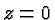 this
definition would give
this
definition would give 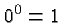 . We also saw that for any natural
number
. We also saw that for any natural
number 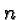 we have that
we have that 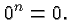 . If we were to expand
that rule to
. If we were to expand
that rule to 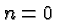 we would have
we would have 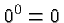 . So we obtain
different value of
. So we obtain
different value of 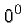 , depending on which rule we want to apply.
In this case, neither rule is better than the other, and so the most
useful approach is to resign ourselves to the fact that
, depending on which rule we want to apply.
In this case, neither rule is better than the other, and so the most
useful approach is to resign ourselves to the fact that 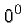 is undefined. There is no problem when the base is non-zero however,
and so we define
is undefined. There is no problem when the base is non-zero however,
and so we define
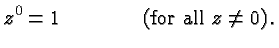
Rational Exponents
Now suppose the exponent is a fraction of the form
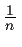 . Again, our central rule applies. We have, for
example,
So
. Again, our central rule applies. We have, for
example,
So
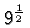 must
be a number which gives
must
be a number which gives 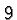 when multiplied with itself. Things now
get a little murky. There are two such numbers, namely
when multiplied with itself. Things now
get a little murky. There are two such numbers, namely 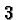 , and
, and
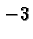 . By convention we pick the positive one:
. By convention we pick the positive one:
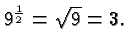 This convention is used everywhere in
the world, but it does lead to confusion. For example, when we solve
equations we may be interested in all solutions and simply evaluating
a square root may cause us to miss some. The only way to handle this
effectively is to understand the issues and to be aware and alert when
solving problems.
Consider another example:
Here there is only one number with that property:
This convention is used everywhere in
the world, but it does lead to confusion. For example, when we solve
equations we may be interested in all solutions and simply evaluating
a square root may cause us to miss some. The only way to handle this
effectively is to understand the issues and to be aware and alert when
solving problems.
Consider another example:
Here there is only one number with that property:
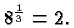 In general we define
where
In general we define
where
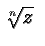 to the power
to the power 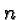 equals
equals 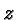 . There is no such (real)
number when
. There is no such (real)
number when 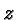 is negative and
is negative and 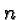 is positive, and so for the
time being we consider
is positive, and so for the
time being we consider
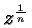 undefined in that case.
There are two such numbers when
undefined in that case.
There are two such numbers when 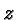 is positive and
is positive and 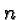 is even,
and in that case we pick the positive such number.
Suppose now that the exponent is a rational number whose
numerator is different from 1. In that case our central rule tells us
immediately what to do. For example,
In general, for natural numbers
is even,
and in that case we pick the positive such number.
Suppose now that the exponent is a rational number whose
numerator is different from 1. In that case our central rule tells us
immediately what to do. For example,
In general, for natural numbers 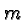 and
and 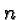 , and
, and 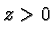 :
For example,
:
For example,
Negative Exponents
Next let's ask what a power should be if the exponent is
negative. According to our central rule
we should have, for example,
So our unknown number 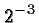 gives
gives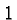 when multiplied with
when multiplied with
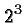 . We have no choice but define
. We have no choice but define
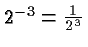 . In general we define, for
. In general we define, for 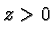 and
any rational exponent
and
any rational exponent 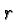 :
For example,
So the next time you go to a party, mention casually that you
finally understand that there is just no way that
:
For example,
So the next time you go to a party, mention casually that you
finally understand that there is just no way that
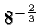 could equal anything other than positive one fourth. You will be the
center of the conversation, and you might steer more students towards
our Math 1010 classes!
could equal anything other than positive one fourth. You will be the
center of the conversation, and you might steer more students towards
our Math 1010 classes!
Irrational Exponents
Defining powers for irrational exponents is beyond the scope of this
class. However, the basic idea is to obtain a sequence of rational
numbers that approaches the irrational exponent, to compute the
corresponding powers, and to define the power to be that number that
is approached by the powers with rational exponents.
Rules and Regulations
Intermediate Algebra Textbooks usually list tables of rules satisfied
by powers. For example, it is true that
It does not pay to
memorize those rules. They all flow from the original definition and
the central rule. If you are unsure whether or not you can do a certain thing
just ask yourself if it works when the exponents are natural numbers
and you use the original definition of powers by repeated
multiplication. If you think in those terms, and you do a few
exercises, you will quickly learn how to work with powers confidently
and effectively.


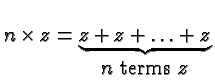
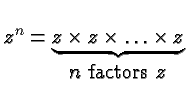
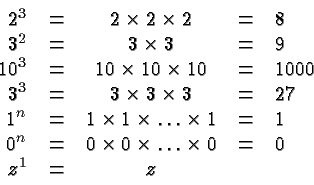

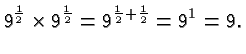
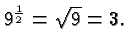 This convention is used everywhere in
the world, but it does lead to confusion. For example, when we solve
equations we may be interested in all solutions and simply evaluating
a square root may cause us to miss some. The only way to handle this
effectively is to understand the issues and to be aware and alert when
solving problems.
Consider another example:
This convention is used everywhere in
the world, but it does lead to confusion. For example, when we solve
equations we may be interested in all solutions and simply evaluating
a square root may cause us to miss some. The only way to handle this
effectively is to understand the issues and to be aware and alert when
solving problems.
Consider another example: