Department of Mathematics --- College of Science --- University of Utah

Mathematics 1010 online

Percent

The word percent means per hundred. You divide something into 100 equal parts and then consider so many parts of it.

The key word here, and the item that causes the greatest confusion in percentage calculations, is "something" . The something of which you calculate a certain number of percent is rarely identified as such explicitly, and it often changes even within the same problem.

Consider this example. Suppose you earn $10.- an hour and you receive a raise of 20%, followed by another raise of 20%. The first raise applies to your hourly wage of $10.-, and the second to your new hourly wage. 20% of $10 is $2.- and so your new hourly wage is $12.-. Your second raise is 20% of $12, which is $2.40, and so your hourly wage after your second raise is $14.40. Note the phrase you receive "a raise of 20%". It's pretty clear that it's 20% of your current salary, and not your CEO's salary, or the gross national product, but that fact is not stated explicitly. Notice also that even though both raises are 20%, they translate into different dollar amounts because they are applied to different hourly wages.

Of course we all know that raises of 20% are all too rare...

Here is another example along the same lines: If you make a certain income, and you receive a raise of 100%, followed by a pay cut of 100%, then your new income is not what you started with, but rather it is zero!

It is possible to have more than 100 percent of something. For example, your boss probably makes more than 100 percent of your income.

To make progress let's introduce some language. The number of which we compute the percent (first $10, and then $12 in the above example) is called the base number. The number of percent (20 in the above example) is the rate, and the rate applied to the base number is the part. Depending on the application the part can have many different names. For example, when the problem is about money, it could be a raise, a discount, a fee, a commission, .etc.

Denoting the part by , the rate by , and the base number by , the basic equation governing all percent calculations is

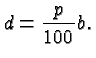
$\displaystyle d = \frac{p}{100}b.$

If you understand this one equation, and you understand and appreciate that the base number is often specified only implicitly, and sometimes not very clearly, then you will able to solve all percent problems that you'll encounter in this class!

Percentage problems differ by what is known and what is to be determined, and, to reiterate, their difficulty usually stems from describing the base number only implicitly. Another source of difficulty is that usually the part is not of interest in itself, but it needs to be added or subtracted to the base number to get the result of interest. In the above example, you are probably more interested in your hourly income after the raise than in the raise itself. The following examples illustrate situations in which one of the three key ingredients is unknown:

Unknown part. You buy a computer at a 25% discount. The base (list) price is $2,000. What is your total price? The base number is 2,000, the rate is 25, and so the part is

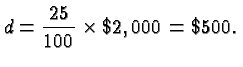
$\displaystyle d = \frac{25}{100}\times \char36 2,000 = \char36 500.$
Your purchase price is

$\displaystyle q = \char 36 2,000 - \char36 500 = \char36 1,500.$
Unknown part. You invest money at an annual interest rate of percent. Interest is paid monthly. Thus every month the bank adds

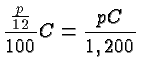
$\displaystyle \frac{\frac{p}{12}}{100}C = \frac{pC}{1,200}$
to which is the amount of money in your account at the beginning of the month. Equivalently, every month your money is multiplied with the factor

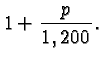
$\displaystyle 1+\frac{p}{1,200}.$
If you invest a penny at 7% interest for 1,000 years, your descendants 1,000 years hence will own

$\displaystyle \char 36 0.01\times \left(1+\frac{7}{1,200}\right)^{12,000} = \char 36 20,525,000,000,000,000,000,000,000,000$
(more than 20 octillion dollars) or thereabouts.
Unknown base number. You buy a car for $18,750 and the dealer informs you that you purchased it at a 25% discount. What is the list price (the base number) of the car? Since we received a 25% discount we purchased the car for 75% of its list price. Denoting the list price by we obtain

$\displaystyle \char36 18,750 = \frac{75}{100}L$
and hence

$\displaystyle L=\char36 18,750 \times \frac{100}{75} = \char36 25,000.$
Unknown Rate. The population of your town is 17,000. A year later it is 17,678. At what (annual) rate is the population growing? The rate satisfies:

$\displaystyle 17,678 - 17,000 = 678 = \frac{p}{100}\times 17,000.$
Hence

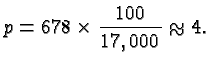
$\displaystyle p = 678 \times \frac{100}{17,000} \approx 4.$
The growth rate in your town is about 4%.

A Complicated Problem

Percentage problems often involve more than one rate, base, and part. I recommend you work through every detail of the following example. It will go a long way to teach you about percent, and it will enable you to calculate your standing and your prospects in this class at any time.

Suppose your WeBWorK homeworks account for 40% of your grade, your midterm exams for 30%, and your final exam also for 30%. (Your actual numbers may be different, of course.) You obtain 90% on your homeworks, 70% on your midterms, and you need to get 80% overall to receive the grade of B+. The maximum point count on the final is 200. How many points do you need to receive (at least) on the final exam so as to obtain a B+ overall?

There are at least four sets of , , and in this problem, your overall score, and one each for homeworks, midterm exams, and the final exam. (In reality these can be broken down farther since there are several homeworks and several midterm exams.) It helps to make things clearer by thinking of the percent you get overall (your primary concern) as something else, like points or cookies. Let's use cookies since points is used for the score on individual assignments. You want to obtain 80 cookies. Your homeworks give you up to 40 cookies, but you get only 90% of those, for a total of 36 cookies. Similarly, the midterms give you 70% of 30 possible cookies, or 21 cookies. So without the final you have 36+21=57 cookies for sure. You need 23 more cookies to get 80 cookies total. The final exam can give you up to 30 cookies, and 23 is 77% of 30. So you need to get at least 77% of the possible final exam score. The maximum possible score is 200 and 77% of 200 is 154. So you need to get at least 154 points on the final to get a B+ in this class. But there is no point in aiming low. So you decide to prepare carefully for the final. Your preparation pays off and you get 200 points, or 100%, or 30 cookies, on the final. Your total in the class is 87 cookies, and you receive the grade of A-. Congratulations!

Another Problem

Here is a problem for you to ponder. E-mail me your answer and your reasoning.

You are commencing a career. Raises in your job are described as percentages of your current salary. Suppose you are going to get a certain set of raises. (If you like and if it helps fix your attention on something like 15%, 10%, 0%, 12%.) Your objective is to maximize your final salary (let's say because it determines your retirement income, and you are going to be a retiree for many decades). In order to obtain this objective, do you want the large raises initially when they apply to small salaries, or do your want them later, when they apply to large salaries? Why? What changes if your objective is to maximize your total earnings rather than your final salary? Summarize the result of your thinking in ten words or less.