Department of Mathematics --- College of Science --- University of Utah

Mathematics 1010 online

Throwing Rocks

If you drop an object on earth, gravity will increase its speed by 32 feet per second every second. Thus after one second it will fall at a speed of 32 feet per second, and after two seconds its speed will be 64 feet per second. We say that gravity is accelerating the object at 32 feet per second per second, or, more concisely, 32 feet per second squared. The particular number 32 is due to the mass of the earth and its radius. It is different on other bodies in the solar system, as indicated in the following table:
 

Earth Moon Sun Mars Venus Mercury
32 5 892 12 29 12 feet/second

 
For generality and clarity let's say that the speed of a falling object increases by $ g $ (where $ g $ stands for gravity) feet per second squared (rather than use the particular number 32). Then the velocity $ v $ after $ t $ seconds is simply $ v(t) = gt. $ It turns out (but is beyond the scope of this class to show) that the distance $ s $ covered by a falling object after $ t $ seconds is given by $ s(t) = \frac{1}{2}gt^2. $ In this formula, the positive direction points down and $ s $ is the depth of an object. More frequently you will find problems that deal with the height of an object which is considered to increase upwards. It turns out that if you release an object at an initial height $ h_0 $ and with an initial velocity $ v_0 $ (which is positive if it points upwards, and negative if points downwards) then the height at time $ t $ is given by

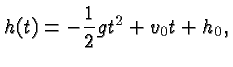
$\displaystyle h(t) = - \frac{1}{2} gt^2 + v_0 t + h_0, $

and the velocity at time $ t $ is given by

$\displaystyle v(t) = - gt + v_0. $

The negative sign in these formulas accounts for the fact that gravity pulls down, but the positive direction is up.

For example, if you toss a rock upwards at an initial velocity of 20 feet per second, and you release it at a height of 5 feet, then its height is described by

$\displaystyle h(t) = -16t^2 + 20t + 5. $

If you wish to know when the rock hits the ground (where the height is zero) you solve the quadratic equation

$\displaystyle -16t^2 + 20t + 5 = 0 $

which gives $ t \approx 1.46 $ seconds.

Suppose now that in addition to tossing that rock upwards you also toss it forward, let's say at a (horizontal) speed of 25 feet per second. You wonder how far that rock will fly. The horizontal and the vertical components of the rock's motion are independent, and since no horizontal force acts on the rock (ignoring air resistance) its forward velocity is constant. Thus the rock flies a distance of $ 1.46 \times 25 \approx 36.5 $ feet before it hits the ground.

Figuring out how high the rock will fly is a little more tricky. You will learn effective ways of answering questions like this in Calculus. At this stage the easiest way to compute the maximum height is to complete the square. We have

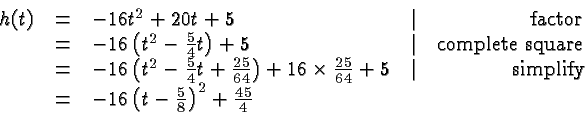
\begin{displaymath} \begin{array}{rclcr} h(t) &=& -16t^2 + 20t + 5 &\vert& \hbox... ...-16\left(t-\frac{5}{8}\right)^2 +\frac{45}{4} \\ \end{array} \end{displaymath}

This may seem a contrived way to write the expression for $ h(t) $. However, it is clear that $ h(t) $ is as large as it can be when the square is zero, i.e., $ t = \frac{5}{8} $. At that time the height is

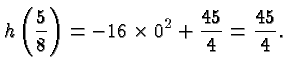
$\displaystyle h\left(\frac{5}{8}\right) = -16\times 0^2 + \frac{45}{4} = \frac{45}{4}. $

The rock reaches a height of 11 feet and 3 inches.

To determine the maximum you could also first ask at what time the vertical velocity is zero, and then evaluate the height at that time.

Summary

To determine the time at which an object is at a particular height you solve a quadratic equation obtained from the height formula. In particular, to find the time an object hits the ground you set the height to zero. To find the maximum height complete the square or ask when the vertical velocity is zero. To find a distance first find the time at which an object hits the ground, and then multiply the horizontal velocity with that time.

Disclaimer

The discussion on this page is fundamentally flawed by the fact that it ignores air resistance. It also ignores the fact that the earth is spherical rather than planar. The formulas on this page are approximately valid for small speeds and heights, and for the purposes of the exercises in this class we will ignore air resistance and the shape of the earth.