

A quadratic equation can be written in the standard form
To solve the quadratic equation means to find values of ![]() that
make the equation true.
To illustrate the principles and issues let's look at a special case
first. Consider the equation
that
make the equation true.
To illustrate the principles and issues let's look at a special case
first. Consider the equation
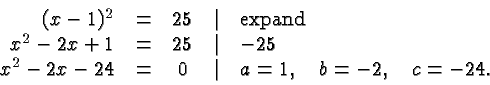
The last equation in this sequence is in standard form, with ![]() ,
,
![]() , and
, and ![]() having the given values. However, the equation
having the given values. However, the equation
![]() can be solved much more easily than
can be solved much more easily than
![]() :
:
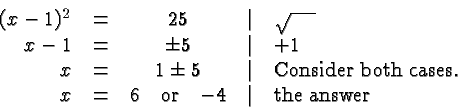
Thus there are two solutions of the equation, ![]() and
and ![]() .
We can (and should) verify this by substituting these values in the
original equation. If
.
We can (and should) verify this by substituting these values in the
original equation. If ![]() we obtain
we obtain ![]() and if
and if ![]() we obtain
we obtain
![]() .
.
Note the symbol ![]() in the second and third of the above sequence
of equations. The square root of
in the second and third of the above sequence
of equations. The square root of ![]() is positive by convention and
equals
is positive by convention and
equals ![]() . However, our task at that stage is not to compute a
square root as such, but to answer the question for what values of
. However, our task at that stage is not to compute a
square root as such, but to answer the question for what values of
![]() does
does ![]() equal
equal ![]() ? There are two such values,
? There are two such values,
![]() and
and ![]() , and we must consider both possibilities.
, and we must consider both possibilities.
Let's now consider the more general equation
It can be solved just like the special case considered earlier:
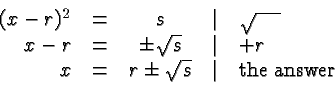
The key to solving quadratic equations is to convert them to
the form ![]() . This process is called completing the
square. It is based on the first and second
binomial formulas .
. This process is called completing the
square. It is based on the first and second
binomial formulas .
Let's see how this works with our equation in standard form:
If the constant term was ![]() instead of
instead of ![]() we would have a
perfect square . To make it so we just add
we would have a
perfect square . To make it so we just add ![]() on both sides and obtain
on both sides and obtain
Note that since
An example illustrates the process:
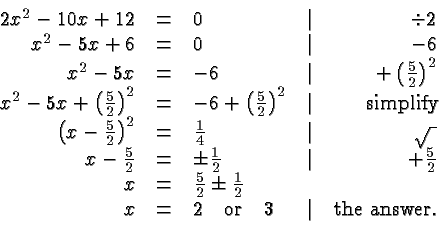
We easily check that ![]() and
and ![]() do in fact satisfy the
original equation.
do in fact satisfy the
original equation.
The above example illustrates one of three possible outcomes of this procedure, the case where there are two real solutions.
In the following example there is only one solution:
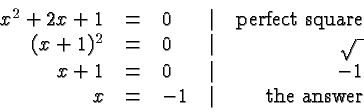
The reason there is only one solution is the fact that there is one
and only one number whose square is ![]() .
.
If the above procedure leads to taking the square root of a negative number we obtain a conjugate complex pair of solutions as illustrated in the following example:
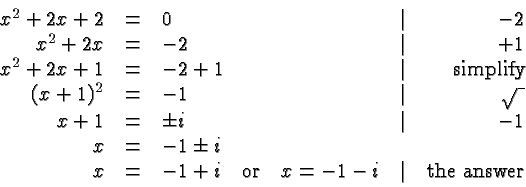
The Quadratic Formula
Of course there is nothing to stop us from applying this procedure
to the
general
equation ![]() . This gives rise to
the quadratic formula .
Personally, I prefer not to burden my mind with having to memorize
reliably yet another formula, and so I complete the square almost
every
time I solve a quadratic equation.
. This gives rise to
the quadratic formula .
Personally, I prefer not to burden my mind with having to memorize
reliably yet another formula, and so I complete the square almost
every
time I solve a quadratic equation.