Department of Mathematics --- College of Science --- University of Utah

Mathematics 1010 online

The Binomial Formulas

The binomial formulas are

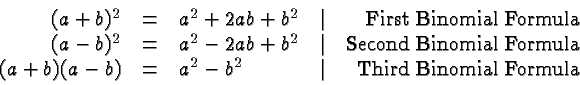
\begin{displaymath} \begin{array}{rclcr} (a+b)^2 &=& a^2+2ab + b^2 &\vert& \hbox... ...a^2-b^2 &\vert& \hbox{Third Binomial Formula} \\ \end{array} \end{displaymath}

$ a $ and $ b $ may be any variables, or even more general expressions. The expression on the left of the first and second binomial formulas are perfect squares, the expression on the left of the third formula is the difference of (two) squares.

Note that the first and second binomial formulas are equivalent. Just replace $ b $ with $ -b $ to get from one to the other.

It is straightforward to verify the binomial formulas from left to right using the distributive law. For example:

$\displaystyle (a+b)^2 = a(a+b)+b(a+b) = a^2 +ab + ba + b^2 = a^2+2ab+b^2. $

However, the power of the binomial formulas arises from being able to read them from right to left. Some examples will illustrate this. In each case look at the right expression and think about how to write it either as a perfect square (as in the first and second binomial formula) or a product of a sum and difference, as in the third binomial formula. Fill in the blank space on the left. This page does not give the answers, however, click here if you get stuck or you want to check your answers.

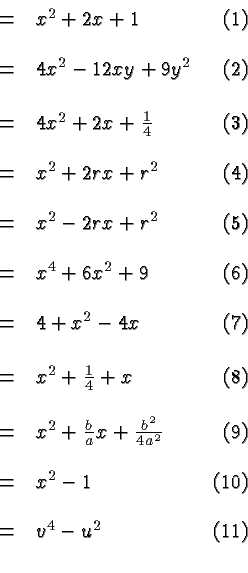
\begin{displaymath} \begin{array}{rclr} \phantom{ (x+1)^2 } &=& x^2+2x+1 & (1) \... ...ntom{ (v^2-u)(v^2+u) } &=& v^4-u^2 & (11) \\ \\ \end{array} \end{displaymath}

Of the above, equations $ (1) $, $ (4) $, $ (5) $, $ (7) $, and $ (8) $ are typical for the kind of operations that occur in the solution of quadratic equations. The equation $ (9) $ describes a critical step in the derivation of the quadratic formula . The other equations described steps that may occur in factoring

You can find many more examples in any textbook on Intermediate Algebra. Look for terms like solving quadratic equations, binomial formulas, perfect squares, completing the square.