Department of Mathematics --- College of Science --- University of Utah

Mathematics 1010 online

The Quadratic Formula

Consider the standard form of a quadratic equation:

$\displaystyle ax^2 + bx + c = 0.$

We can solve this general equation by completing the square exactly like we would solve it if the coefficients assumed specific values:

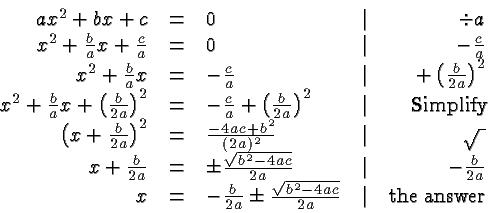
$\begin{displaymath} \begin{array}{rclcr} ax^2+bx+c &=& 0 &\vert& \div a \\ x^2... ...\sqrt{b^2-4ac}}{2a} &\vert& \hbox{the answer} \\ \end{array} \end{displaymath}$

The last of these equations is the celebrated quadratic formula. It can also be written as:

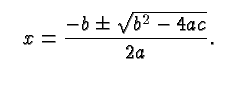
$\displaystyle \quad x= \frac{b \pm\sqrt{b^2-4ac}}{2a}.\quad \vphantom{{\frac{b \pm\sqrt{b^2-4ac}}{2a}}^2_2}$

Notice the term

$\displaystyle D=b^2-4ac$

under the square root. It determines the number of solutions of

and their nature, and is called the Discriminant of

Clearly there are three cases:

$\begin{displaymath}D\phantom{s} \begin{cases} > 0 & \hbox{there are two real sol... ...ere is a conjugate complex pair of solutions.}\\ \end{cases} \end{displaymath}$

To apply the quadratic formula to a particular quadratic equation just convert the equation to standard form and substitute the appropriate values of , and in the formula. However, I believe it is more efficient and less error prone to make sure you understand the binomial formulas and the concept of completing the square and to solve a quadratic equation from scratch whenever you need to. Memorizing facts like the quadratic formula quickly becomes tedious and your memory may fail at an inopportune moment. On the other hand, there are of course formulas--like the distributive law , the binomial formulas, and the rules for manipulating powers --that you should be able to remember, but you do so because these formulas are simple and you use them so frequently that they become part of your consciousness.