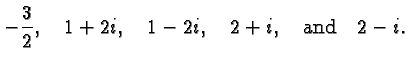It's obvious that a polynomial such as
Suppose we recognize, for example by trial and error, or drawing a graph, that the polynomial
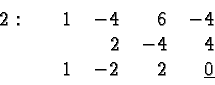
This means that
To find the remaining zeros of ![]() we only have to find the zeros of
we only have to find the zeros of
![]() . This means we have to solve the
quadratic equation
. This means we have to solve the
quadratic equation
Thus we see that the roots of ![]() are
are ![]() and
and ![]() , and
we were able to find all of them once we recognized one of them. In
general, if we have a polynomial
, and
we were able to find all of them once we recognized one of them. In
general, if we have a polynomial ![]() and one real root we can use
synthetic division to obtain a polynomial of degree one less whose
roots equal the remaining roots of
and one real root we can use
synthetic division to obtain a polynomial of degree one less whose
roots equal the remaining roots of ![]() .
.
Suppose the complex number ![]() is a root of a polynomial
is a root of a polynomial ![]() . Then
we can write
. Then
we can write
![]() just as above. However, the
coefficients of
just as above. However, the
coefficients of ![]() are complex numbers even if the
coefficients of
are complex numbers even if the
coefficients of ![]() are real numbers. The process still works, but
it requires complex arithmetic, and there is a better way that uses
real arithmetic only.
are real numbers. The process still works, but
it requires complex arithmetic, and there is a better way that uses
real arithmetic only.
The key fact in this context is that conjugate
complex ![]() of
of ![]() is also a root of
is also a root of ![]() .
It's a simple exercise to see that this is true by observing that the
conjugate complex of a real number is the number itself, and that for
any complex numbers
.
It's a simple exercise to see that this is true by observing that the
conjugate complex of a real number is the number itself, and that for
any complex numbers ![]() and
and ![]()
Thus if ![]() is a factor of
is a factor of ![]() then
then ![]() is also a
factor, and so is the product
is also a
factor, and so is the product
![]() . This last term is
a quadratic polynomial whose coefficients are real. To see this
let
. This last term is
a quadratic polynomial whose coefficients are real. To see this
let
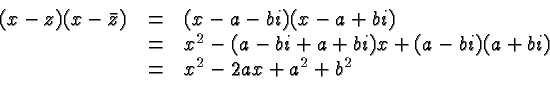
Hence if we know that ![]() is a root of
is a root of ![]() then
then ![]() is
also
a root and we can obtain a polynomial
is
also
a root and we can obtain a polynomial ![]() satisfying
satisfying
Let's look again at the above example. Essentially we work it backwards. Again, let
We know that ![]() is a root of
is a root of ![]() . Thus
. Thus ![]() and
and
![]() So we can write
So we can write
The following example shows all the principles described above in action. It does not address the question of how one might find a particular root. The answer to that question depends on the context in which the polynomial in question occurs. There are general purpose methods for finding a single root but they are beyond the scope of this class.
Let
It is easily checked that
![]() is a root of
is a root of ![]() . This means that
. This means that
![]() is
a factor of
is
a factor of ![]() . We find it by
synthetic
division :
. We find it by
synthetic
division :
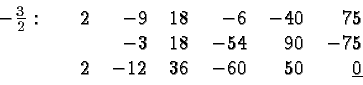
Hence
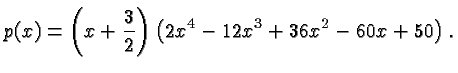
Note that the remainder of the division by
![]() is zero (underlined in the above table) which confirms that
is zero (underlined in the above table) which confirms that
![]() is in fact a root.
is in fact a root.
![]() can be rewritten (after multiplying first factor and dividing the
second factor by 2) as
can be rewritten (after multiplying first factor and dividing the
second factor by 2) as
We now need to find the roots of
It turns out that ![]() is a root of
is a root of ![]() .
.
Thus
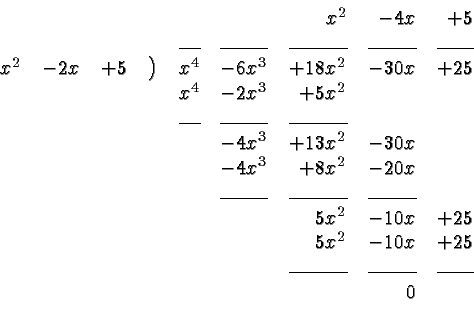
Again, the fact that the remainder is zero indicates that
![]() is actually a factor of
is actually a factor of ![]() . In fact,
. In fact,
The roots of the first factor are ![]() , that's how we
constructed that factor. The roots of the second factor can be found
by solving the quadratic equation
, that's how we
constructed that factor. The roots of the second factor can be found
by solving the quadratic equation