

Roots and Radicals deserve their own chapter and homework because they occur frequently in applications.
Let ![]() be a
natural number , and let
be a
natural number , and let ![]() be a
real number . The
be a
real number . The ![]() -th root of
-th root of
![]() is a number
is a number ![]() that satisfies
that satisfies
![]() The number
The number ![]() is denoted by
is denoted by
For example,
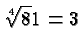 since
since ![]() , and
, and
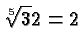 since
since ![]() .
.
The symbol
![]() is called the radical symbol, and
an expression involving it is called a radical (expression).
is called the radical symbol, and
an expression involving it is called a radical (expression).
If ![]() then
then ![]() is the square root of
is the square root of ![]() and the number
and the number ![]() is usually omitted. For example,
is usually omitted. For example,
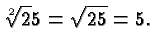
If ![]() , then
, then ![]() is the cube root of
is the cube root of ![]() . For example,
the cube root of
. For example,
the cube root of ![]() is
is ![]() , and that of
, and that of ![]() is
is ![]() .
.
If ![]() is even and
is even and ![]() is positive then there are two
is positive then there are two ![]() -th
roots of
-th
roots of ![]() , each being the negative of the other. For example,
since
, each being the negative of the other. For example,
since
![]() there are two square roots of
there are two square roots of ![]() . In
that case by convention the symbol
. In
that case by convention the symbol
![]() means the positive
means the positive
![]() -th root of
-th root of ![]() , and it is called the principal (
, and it is called the principal (![]() -th) root
of
-th) root
of ![]() .
.
If ![]() is negative and
is negative and ![]() is odd then there is just one
is odd then there is just one ![]() -th root, and it is negative also. For example,
-th root, and it is negative also. For example,
![]()
At this stage we do not know of an ![]() -th root if
-th root if ![]() is even
and
is even
and ![]() is negative. This leads to the subject of
complex numbers which we will take up later in the course.
is negative. This leads to the subject of
complex numbers which we will take up later in the course.
Radicals are just special cases of powers, and you can simplify much of your thinking by keeping this fact in mind:
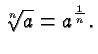
It follows immediately from that observation and the properties of powers that
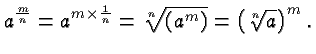
An equation involving radicals is called a radical equation
(naturally).
To solve it you simply apply our general
principle:
To solve an equation figure out what bothers you and then do the same
thing on both sides of the equation to get rid of it.
To get rid of a radical you take it to a power that will change
the rational exponent to a natural number. This will work if the
radical is on one side of the equation by itself.
Let's look at a few simple examples:
Suppose
Here is a slightly more complicated problem:
Our last example shows how to get rid of more than one radical:
To get rid of the square roots we isolate them and square one at a
time:
In each case, we check our answer by substituting it in the original
equation.
For example, in the last equation we obtain:
Later in the course we will consider more complicated cases of
radical equations.
The radicals in the above examples were all natural numbers.
This is due only to a judicious choice of examples. Frequently the roots
occurring in applications are irrational numbers with decimal expansions that never repeat or terminate. The following table lists approximations of
a few specific radicals.
Solving Radical Equations
![]()
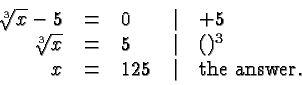
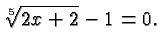
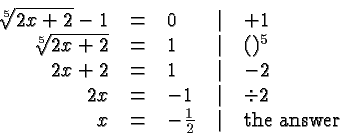
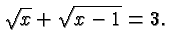
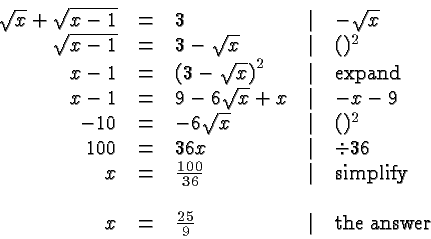
Numerical Values
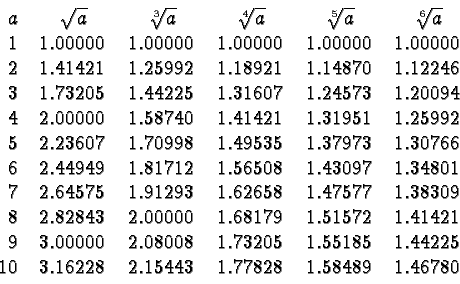
Some Radicals (Approximately)