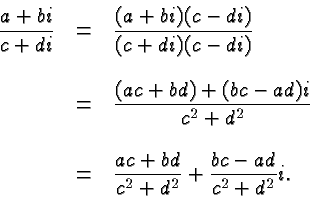We have to expand the numbers system one more time, to include complex numbers. Unfortunately it is not easy to motivate this expansion as compellingly as the previous expansions. Complex numbers have a tremendous range of applications, that will become apparent as you move on in Mathematics, Science, and Engineering, but they may be hard to appreciate at this stage.
For our purposes we start with the observation that there is no real
number ![]() such that
such that
We now take a leap of faith the kind of which sometimes gives
mathematics a bad name. We don't know of a number satisfying the
above equation, so we stipulate that there is a solution and we give
it a name. We call
it ![]() .
.
There are only two things about ![]() we need to know and appreciate. One is the
fact that
we need to know and appreciate. One is the
fact that
The second fact is that we define the arithmetic operations with ![]() such that the ordinary rules of arithmetic continue to hold.
such that the ordinary rules of arithmetic continue to hold.
Let's consider some consequences of this fact. We obtain in particular
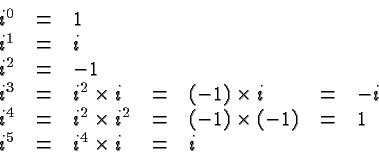
Let's take stock and introduce some language. The symbol ![]() is
called the imaginary unit. A complex number
is
called the imaginary unit. A complex number ![]() is an
expression that can be written in the form
is an
expression that can be written in the form ![]() where
where ![]() and
and
![]() are real numbers (and
are real numbers (and ![]() multiplies
multiplies ![]() ). That particular
form is sometimes called the standard form of a complex number.
). That particular
form is sometimes called the standard form of a complex number.
![]() is called the real part of
is called the real part of ![]() , and
, and ![]() is its
imaginary part. If the real part of
is its
imaginary part. If the real part of ![]() is zero, and the imaginary
part non-zero, then
is zero, and the imaginary
part non-zero, then ![]() is called an imaginary number. (If
the imaginary part is zero, then
is called an imaginary number. (If
the imaginary part is zero, then ![]() is a real number.) If you
want to emphasize that the real part is zero you can call the number
pure imaginary or purely imaginary.
is a real number.) If you
want to emphasize that the real part is zero you can call the number
pure imaginary or purely imaginary.
Note that the imaginary part of a complex number is in fact a real number (and not, as you might reasonably expect, an imaginary number).
Consider, for example, the complex number
![]() . Its real
part is
. Its real
part is ![]() , and its imaginary part is
, and its imaginary part is ![]() . The number
. The number
![]() is also a complex number. Its standard form is
is also a complex number. Its standard form is ![]() , its real part
, its real part ![]() , and its imaginary part
, and its imaginary part ![]() . The
number
. The
number ![]() is imaginary, the number
is imaginary, the number ![]() is real. Both numbers
are complex. In fact, all real numbers and all imaginary
numbers are complex. On the other hand, some complex numbers are real,
some are imaginary, and some are neither.
is real. Both numbers
are complex. In fact, all real numbers and all imaginary
numbers are complex. On the other hand, some complex numbers are real,
some are imaginary, and some are neither.
(A small aside: The textbook defines a complex number to be imaginary
if its imaginary part is non-zero. According to that definition an
imaginary number may have a non-zero real part. For example, the
number ![]() would be imaginary. That definition is non-standard. I
expect it's just a mistake. In any case you should not adopt that
definition, it is not useful.)
would be imaginary. That definition is non-standard. I
expect it's just a mistake. In any case you should not adopt that
definition, it is not useful.)
The fact that some numbers are imaginary does not mean that they are inferior or mysterious, or somehow less than real. It just means they are complex numbers whose real part is zero. The word real in this context emerged in the course of history, but its modern meaning in our context is quite different from the meaning of "realistic". As far as a mathematician is concerned, real, imaginary, and complex numbers are all equally "realistic".
Here is one of the principles that make understanding mathematics possible:
You work with complex numbers as you would with ordinary algebraic
expressions containing the variable ![]() , except that you
replace
, except that you
replace ![]() with
with ![]() wherever it occurs.
wherever it occurs.
Let's look at the four basic operations. For the sake of illustration
we'll combine the complex numbers ![]() and
and ![]() . We'll
also give the general formulas but you don't have to memorize them since
the principle given in the previous paragraph tells you (almost)
everything you need to know.
. We'll
also give the general formulas but you don't have to memorize them since
the principle given in the previous paragraph tells you (almost)
everything you need to know.
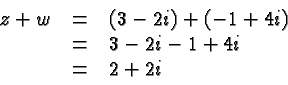
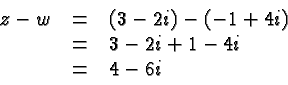
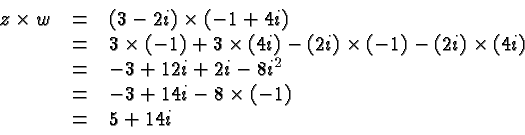
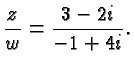
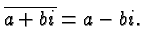
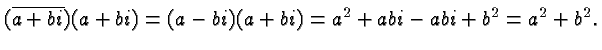
We now return to the problem of dividing two complex numbers. We are bothered by the complex number in the denominator and we get rid of it by multiplying with its conjugate complex in the numerator and denominator. Hence
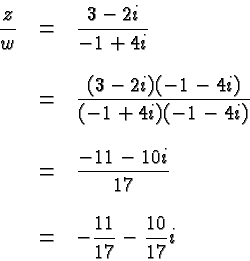
In general we have