Department of Mathematics --- College of Science --- University of Utah

Mathematics 1010 online

Scaling Rules!

Some of the word problems in this class deal with the effects of scaling. Scaling an object means multiplying every linear dimension of it by the same factor. Thus you change the size of the object, but not its shape. The laws of scaling described on this page explain why there are no giants or dragons, why animals can't fly if they weigh more than 50 pounds or so, why a spider can jump out of an airplane without getting hurt while an elephant would be likely to break some bones if he jumped off a table, why stars are spherical, why potatoes cook quicker if you cut them into pieces, why kids get cold more easily than adults, why basket ball players weigh so much, why the largest animals (blue whales) that ever lived live in water, and a host of other every day phenomena. Moreover, analyzing the effects of scaling is an excellent exercise in using radicals and powers .

While of course most objects and creatures have complicated shapes, everything about scaling can be understood in terms of cubes. You can think of any other object as having been composed of many small cubes. When you scale the object, whatever happens to each of the small cubes also happens to the object as a whole. So if you understand cubes you understand almost everything about scaling!

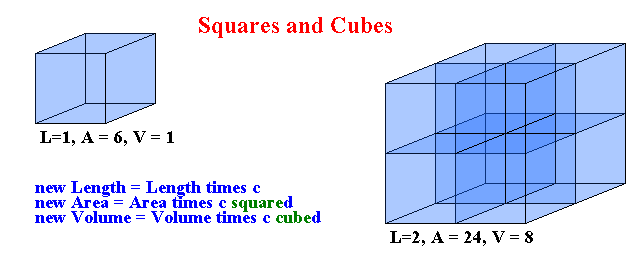
As indicated on the left in this Figure, consider a cube that's one inch long, one inch wide, and one inch high. The area of each of its six square faces is one square inch, and since it has six faces its total (surface) area is six square inches. The volume of the cube is one cubic inch. That's where the words square in square inch and cubic in cubic inch come from!

If we multiply the length, width, and height of that cube with two, say, we obtain a new cube, shown on the right in the Figure. It's bigger, but it's a cube, it has the same shape as the original, smaller, cube. As the Figure shows, we can think of that new cube as having been obtained by piling up eight of the old cubes in two layers of four cubes each. The volume of the larger cube, therefore, is eight cubic inches, eight times the volume of the smaller cube. The area of each face of the new and larger cube is four square inches, and so its total area is $ 24 $ square inches, four times the area of the original cube. In building the larger cube, we multiplied the length of the cube with $ 2 $, its area with $ 4=2^2 $ , and its volume with $ 8 = 2^3 $.

More generally consider a cube of length $ L $. Its volume equals $ v=L^3 $. Notice the exponent 3. This is why we use the phrase cubed to express a third power. It's what we need to compute the volume of a cube.

Similarly, each of the six square faces of cube has an area of $ L^2 $. That's why we use the word squared to denote a second power, we need it to compute the area of a square. The total area of the cube is $ a=6L^2 $. Now consider multiplying the length (and width and height) of that cube with a factor $ c $. We obtain a new cube of length, width, and height $ cL $. Its volume is

$\displaystyle V=(cL)^3 = c^3L^3 = c^3v, $

and its area is

$\displaystyle A = 6(cL)^2 = 6 c^2 L^2 = c^2a. $

So when we multiply the length with $ c $ we multiply the area with $ c^2 $ and the volume with $ c^3 $.

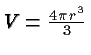This is true not just for cubes. We could do a similar analysis for a sphere of radius $ r $. Its volume equals $ v=\frac{4\pi r^3}{3} $ and its area equals $ a=4\pi r^2. $ Note the factors $ r^3 $ and $ r^2 $. As before, if we multiply $ r $ with a factor $ c $ we multiply the volume with $ c^3 $ and the area with $ c^2 $.

This is true in great generality. As mentioned above, just think of a general object as being approximated by many small cubes, and think about what happens to each of these little cubes as we scale its length by a factor $ c $.

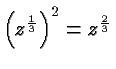What about multiplying something other than length? It follows from our discussion that if we multiply the volume (rather than all lengths) of an object with a factor $ z $, then we multiply each linear dimension (length) with $ 3^\frac{1}{3} $ and each area with $ \left(z^\frac{1}{3}\right)^2 = z^\frac{2}{3} $. If we were to multiply the area with a factor $ z $ we'd have to multiply each linear dimension with $ \sqrt{z} $ and the volume with the cube of that factor, i.e., $ z^\frac{3}{2} $. These facts are summarized in the following Table

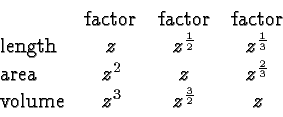
\begin{displaymath} \begin{array}{lccc} &\hbox{factor}&\hbox{factor}&\hbox{facto... ...} \\ \hbox{volume} & z^3 & z^{\frac{3}{2}} & z\\ \end{array} \end{displaymath}

To use the table find the column that contains a $ z $ for the quantity (length, area, or volume) that gets multiplied with a known factor. The other two quantities are multiplied with the factor given in that column. So for example, if you know that the area is multiplied with $ 2 $ then you look at the second column headed factor and use $ z=2 $. 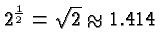The other entries in the column tell you that the weight is multiplied with $ 2^{\frac{3}{2}}\approx 2.828 $ and the length is multiplied with $ 2^{\frac{1}{2}} = \sqrt{2} \approx 1.414 $. Remember that quantities like weight go with volume, and paint goes with area.

Of course, you don't need to memorize that table. Everything flows from the fact that areas get multiplied with the square, and volumes with the cube, of whatever factor multiplies the lengths.