Department of Mathematics --- College of Science --- University of Utah

Mathematics 1010 online

More on Linear Systems

Number of Solutions

Most linear systems you will encounter will have exactly one solution. However, it is possible that there are no solutions, or infinitely many. (It is not possible that there are exactly two solutions.)

Let's take a closer look. It never hurts in any investigation to look at the simplest possible case first. So consider again the single equation

$\displaystyle ax=b\qquad(*) $

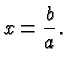
where $ a $ and $ b $ are parameters and $ x $ is the variable whose value needs to be determined. There are three possible cases:

  1. $ a\neq 0: $ In this case dividing by $ a $ on both sides of $ (*) $ gives the unique solution

    $\displaystyle x= \frac{b}{a}. $

    The word unique in this context means there is a solution, and it's the only one.

  2. $ a=0 $ and $ b\neq 0 $. In this case $ (*) $ turns into $ 0=0x=b\neq 0 $. Since $ 0\neq 0 $ is impossible there is no solution.

  3. $ a=0 $ and $ b=0 $. In that case $ (*) $ turns into $ 0x=0 $ which is true for all numbers $ x $. There are infinitely many solutions.

It is clear since we cover all possibilities above that it is impossible for the $ (*) $ to have precisely $ 2 $, or $ 3 $, or any finite number, of solutions. Compare this for example with quadratic equations which may have $ 0 $, $ 1 $, or $ 2 $, but never any other number of (real) solutions.

Next Consider two equations in two unknowns, let's say

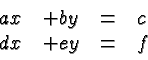
\begin{displaymath} \begin{array}{rrcl} ax & + by &=& c \\ dx & + ey &=& f\\ \end{array} \end{displaymath}

Each of these two equations defines a line in the cartesian plane . All solutions are the coordinates of a point where the two lines intersect. There are again three possibilities.

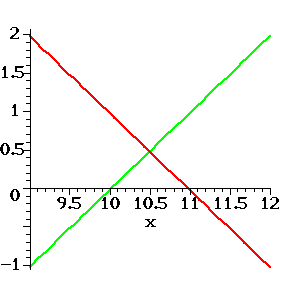
  1. Figure 1: Unique Solution of two equations in two unknowns.

    The lines intersect in one point. There is a unique solution (i..e, the coordinates of that point). An example is provided by

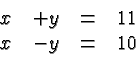
    \begin{displaymath} \begin{array}{rrcl} x & + y &=& 11 \\ x & - y &=& 10\\ \end{array} \end{displaymath}

    The solution is $ x=10.5 $ and $ y=0.5 $, as shown in Figure 1.

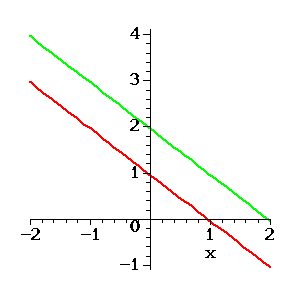
  2. Figure 2: No Solution of two equations in two unknowns.

    The lines are parallel but distinct. They never intersect and there is no solution. An example is provided by

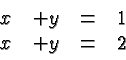
    \begin{displaymath} \begin{array}{rrcl} x & + y &=& 1 \\ x & + y &=& 2 \\ \end{array} \end{displaymath}

    Note that obviously the two equations contradict each other, nothing can simultaneously equal $ 1 $ and $ 2 $.

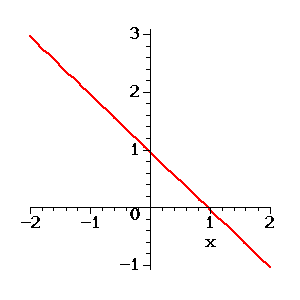
  3. Figure 3: Infinitely many solutions of two equations in two unknowns.

    The lines are identical. Any point on the lines provides a solution. A trivial example can be obtained by writing the same equation twice. A less trivial example is

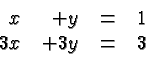
    \begin{displaymath} \begin{array}{rrcl} x & + y &=& 1 \\ 3x & + 3y &=& 3 \\ \end{array} \end{displaymath}

    The second equation follows from the first by multiplying on both sides with 3.

More than two Equations. Similar considerations apply to systems of more than two equations, but this is a subject beyond the scope of this class. You will learn more when you take a class on Linear Algebra.

A Complicated Example

Suppose we want to find a quartic polynomial whose value equals $ 2^x $ for $ x=0,1,2,3,4 $. The purpose of this exercise might be to to approximate $ 2^x $ by a polynomial on a calculator that cannot evaluate $ 2^x $ for non-integer $ x $ directly. Approximating functions is a huge subject, here we just use this problem as an example for a more complicated linear system.

Let's write our quartic polynomial as

$\displaystyle p(x) = e+dx+cx^2+bx^3+ax^4. $

We want it to satisfy the equations

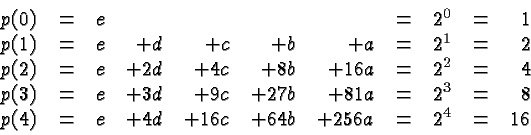
\begin{displaymath} \begin{array}{rcrrrrrcrcr} p(0) & = & e & & & & & = & 2^0 & ... ... +4d & +16c & +64b & +256a & = & 2^4 & = & 16 \\ \end{array} \end{displaymath}

This is a linear system of five equations in the five unknowns $ a $, $ b $, $ c $, $ d $, and $ e $.

The table below is set up as discussed except that whenever an entry is $ 0 $ it is left blank to clarify the reduced systems.

\begin{displaymath} \begin{array}{rrrrrrrrr} \hbox{equation} & & e & d & c & b &... ...{[15] = [14]-4[13]} & & & & & & 24 & 1 & 25 \\ \end{array} \end{displaymath}

Equation $ [1] $ is very special, it tells us right away that $ \underline{e=1} $. We use that equation to eliminate $ e $ from the remaining equations which gives us four equations ($ [6] $ through $ [9] $) in the four unknowns $ a $, $ b $, $ c $ and $ d $.

Equation $ [15] $ is $ 24a=1 $ which means $ \underline{a=\frac{1}{24}} $. Substituting the value of $ a $ into equation $ [13] $ gives $ 36a + 6b = \frac{3}{2} + 6b = 1 $ which implies $ \underline{b = -\frac{1}{12}} $. Substituting $ a $ and $ b $ into equation $ [10] $ gives the equation $ 14a+6b+2c = \frac{7}{12} -{1}{2} + 2c = 1 $ which implies $ \underline{c=\frac{11}{24}} $. Finally, substituting $ a $, $ b $ and $ c $ into equation $ [6] $ gives $ a+b+c+d = \frac{1}{24} -\frac{1}{12} + \frac{11}{24}+d=1 $ which implies $ \underline{d=\frac{7}{12}} $.

Putting the underlined results together (and writing everything over the common denominator $ 24 $) gives

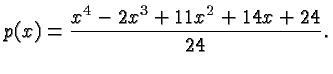
$\displaystyle p(x) = \frac{x^4-2x^3+11x^2+14x+24}{24}. $

Figure 4: A polynomial approximation of $ f(x) = 2^x $.

Figure 4 shows the graph of $ p $ (red) as well as the graph of $ f(x) = 2^x $ (green). It is apparent that $ p $ is a good approximation of $ f $ in the interval from $ 0 $ to $ 5 $. There are other and more effective ways of computing polynomials like $ p $. However, this example illustrates how Gaussian Elimination and Backward Substitution can be used to solve a linear system. In this particular linear system we were fortunate in that the elimination proceeded in a straightforward way without fractional arithmetic. It happens frequently that linear systems have a special structure that can be effectively exploited.

A final word on computing the row sums. They appear to be a waste of effort when the problem is all solved. However, when I first computed the entries in the above table I made several mistakes that I discovered immediately because of the row sums. There is a good chance you will save yourself a lot of time and aggravation by carrying them along in your own calculations.