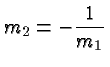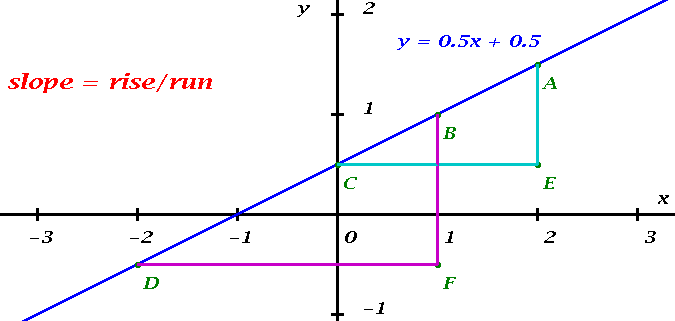
All you need to understand about straight lines is contained in the picture above. Think of moving along the blue line. You climb one unit for every two units that you move to the right. The slope of the line is the ratio of the vertical and the horizontal distances, called rise and run, respectively.
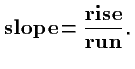
A straight line is characterized by the fact that the slope is independent of where you compute the rise and the run. The two triangles AEC and BFD in the Figure are similar. This means that corresponding angles are equal, and hence the ratios of the lengths of corresponding sides are equal. It does not matter which two points on the line we pick (as long as they are distinct), we will get a similar triangle, and the same slope, for all choices. In the picture, the various points have the following coordinates:
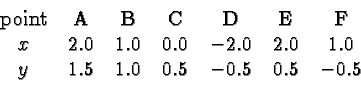
Using the cyan triangle AEC we obtain for the slope ![]() of the line
of the line
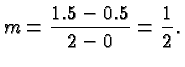
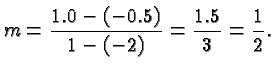
Everything about straight lines flows from the concept of slope. There are some details and some language that you need to be familiar with. But essentially all problems concerning straight lines, certainly in this class, require that you work with the slope of the straight line.
A straight line may be horizontal in which case its slope is zero.
It may be vertical, in which case the definition of slope breaks down
since it calls for a division by zero. We say that the slope is
undefined. It may also descend to the right in which case the slope
is negative. Check here for an
example of a line with a negative slope.
A straight line may intersect the
The line in the above Figure is described by the equation
Suppose we are given two points
If we are given the slope
An equation of the form
Two lines are parallel if their slopes are equal. You can see this
immediately by drawing two parallel lines and triangles like those in
the Figure on this page. All the triangles are similar.
Two lines with slopes
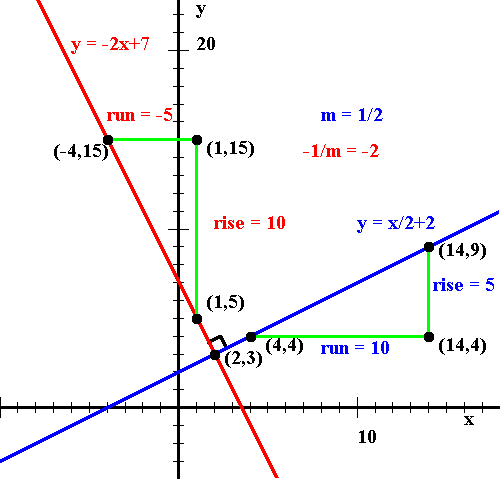
The following Figure explains why the slopes are related in this way:
It shows two perpendicular lines with slopes 1/2 (shown in
blue) and
-2 (shown in red), intersecting in the point (2,3). The
two green triangles are congruent, and the one associated with the red
line can be obtained by rotating by 90 degrees the other triangle
associated with the blue line. If you think of subtracting the
coordinates of the point close to the intersection from those of the
point far away, that rotation turns the original run into the new
rise, and the original rise into the negative of the new run, as
illustrated in the Figure. You can also think of subtracting the
coordinates of the leftmost point from those of the rightmost, in
which case the rise is multiplied with negative 1 and the run
maintains its sign, without affecting the sign of the slope.
Intercepts
![]() and
and ![]() axes, in the
points
axes, in the
points ![]() and
and ![]() , respectively. The numbers
, respectively. The numbers
![]() and
and ![]() are called the
are called the ![]() -intercept and
-intercept and ![]() -intercept of
the straight line, respectively. Note that the intercepts are
numbers, they are not points. For the line illustrated on this page
the
-intercept of
the straight line, respectively. Note that the intercepts are
numbers, they are not points. For the line illustrated on this page
the ![]() intercept =
intercept =
![]() and the
and the ![]() -intercept is
-intercept is
![]() .
.
The Slope-Intercept Form of a line.
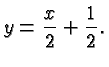
![]() by
by ![]() then
then ![]() increases by
increases by
![]() and so the slope of that line is
and so the slope of that line is
![]() .
When
.
When ![]() then
then
![]() and so the
and so the ![]() -intercept is
-intercept is
![]() . To obtain the
. To obtain the ![]() -intercept we set
-intercept we set ![]() and
solve for
and
solve for ![]() :
:

![]()
![]() and
and ![]() intercept
intercept ![]() . It is
called the slope-intercept form of a line.
. It is
called the slope-intercept form of a line.
The Two-Point-Form of a Straight
Line.
![]() and
and
![]() on a line. Let's denote a general point on the line by
on a line. Let's denote a general point on the line by
![]() . Then, since the slope is independent of the choice of
points we obtain the equation
. Then, since the slope is independent of the choice of
points we obtain the equation
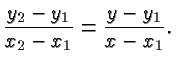
![]() and
and ![]() , as
indicated in the cyan triangle in the above Figure, we obtain the
equation
, as
indicated in the cyan triangle in the above Figure, we obtain the
equation
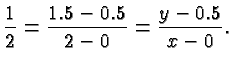
![]() and adding 0.5 on both sides gives the
slope-intercept form.
and adding 0.5 on both sides gives the
slope-intercept form.
The Point-Slope-Form of a Straight
Line.
![]() of a line, and a point
of a line, and a point ![]() on it,
we denote again by
on it,
we denote again by ![]() a general point and obtain
a general point and obtain
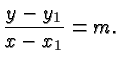
![]() and
and
![]() we obtain for the line
in our Figure:
we obtain for the line
in our Figure:
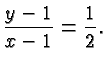
![]() and adding 1 on both sides again gives the
familiar slope intercept form.
and adding 1 on both sides again gives the
familiar slope intercept form.
The general equation of a straight
line.
![]()
![]() ,
, ![]() and
and ![]() are constants defines a straight line.
For example, our line on this page can be written as
are constants defines a straight line.
For example, our line on this page can be written as
![]()
![]() and
and ![]() .
Once again, you can solve for
.
Once again, you can solve for ![]() and obtain the slope-intercept form.
Such a general equation has the advantage of capturing the possibility
of a vertical line (where
and obtain the slope-intercept form.
Such a general equation has the advantage of capturing the possibility
of a vertical line (where ![]() ).
).
Parallel Lines
Perpendicular Lines
![]() and
and ![]() are perpendicular if
are perpendicular if