Department of Mathematics --- College of Science --- University of Utah

Mathematics 1010 online

Linear Systems of Equations

As we have seen before, a linear equation in one variable is an equation of the form

$\displaystyle ax=b\qquad(*) $

where $ a $ and $ b $ are constants, and $ x $ is the variable (also called the unknown in this context) whose value needs to be determined. There is one equation and one unknown.

It is possible to have several unknowns, but then we also have to have several equations. An equation in several unknowns is linear if the unknowns are multiplied with constants and those products add to a constant. A set of linear equations is called a linear system.

The most important and typical case is that the number of equations equals the number of unknowns.

Let's illustrate the concepts with the following simple system. Suppose there are two variables, $ x $ and $ y $, and we have the two equations

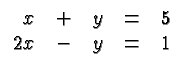
$\displaystyle \begin{array}{rcrccl} x&+&y&=&5\\ 2x&-&y&=&1\\ \end{array}$

We begin by observing that both equations are satisfied if $ x=2 $ and $ y=3 $. This is easy to check (and I know it because that's how I set up the system), but how would we know if nobody told us the solution?

The textbooks usually present two methods of solving a linear system, substitution and elimination. Substitution works by solving one equation for one variable, and substituting its value (in terms of the other variables) in the other equations. It works well for small systems (and it can sometimes be applied successfully to nonlinear systems). Elimination, or Gaussian Elimination, is essentially equivalent, but it's more systematic, and it's the basis of virtually all computer methods of solving large linear systems. This page focuses on elimination.

Consider again the above system. Let's do something that may appear mysterious at first, but that embodies the basic idea. Let's multiply with $ 2 $ on both sides of the first equation. This gives the new system:

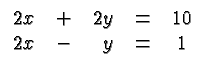
$\displaystyle \begin{array}{rcrccl} 2x&+&2y&=&10\\ 2x&-&y&=&1\\ \end{array}$

The significance of this operation is that in the new system the variable $ x $ has the same coefficient in both equations.

Next, let's subtract $ 10 $ on both sides of the second equation. However, on the left side let's not call it $ 10 $. Let's call it $ 2x+y $. We can do this, according to the first equation. The second equation becomes

$\displaystyle 2x-y - (2x+2y) = 1-10 $

or, after simplifying,

$\displaystyle -3y = -9. $

Dividing by $ -3 $ on both sides gives

$\displaystyle y=3 $

.

Now that we know $ y $ we return to the first equation and substitute $ 3 $ for $ y $. This gives the equation:

$\displaystyle 2x+6=10 $

which has the solution $ x=2 $.

The first step (multiplying with $ 2 $) and the second step (subtracting from the second equation) are usually combined and described, somewhat imprecisely, as subtracting twice the first equation from the second equation.

So in the above example we subtracted a suitable multiple of the first equation to get a new equation that has just one variable. We solved that equation, and then substituted its solution in the first equation which at that stage also turned into a single equation with a single unknown. We finished by solving that single equation.

Remember that at the end of the process we check our answers by substitution. Clearly, substituting $ x=2 $ and $ y=3 $ in the original equations shows that those equations are satisfied.

If we had more than two equations, say $ n $ equations, we would pick a suitable equation (which may be the first, or any other equation) and a particular variable (which may be the first, or another) and subtract suitable multiples of our chosen equation from the other equations so that the chosen variable no longer shows up in the resulting $ n-1 $ equations in $ n-1 $ unknowns. At that stage, we have reduced our problem to a simpler problem of the same structure. We repeat the process until we get a single equation in a single unknown. The process so far is called Gaussian Elimination. We solve our single remaining equation, substitute its solution in an equation that has only two unknowns, solve that one, substitute the two now known variables into an equation with three unknowns, and in this manner work our way backwards until we have all the solutions. This second process is called Backward Substitution.

The method outlined here works in general. For work with paper and pencil it needs to be streamlined. Moreover, it is almost inevitable to avoid mistakes. Mistakes are harmless if they are recognized immediately. Let me describe a procedure that's efficient and that lets you discover errors immediately.

To begin with, we don't need to write down the unknowns all the time. It is sufficient to write down their coefficients. This will save time and effort. To check for errors we keep track of one more number, the row sum of each equation. It is simply the sum of the coefficients and the right hand side of each equation. For example the equation

$\displaystyle x+2y-5z=1 $

has the row sum

$\displaystyle 1+2-5+1 = -1. $

To keep track of the equations we number them and also the new equations. To distinguish row numbers from coefficients let's write them in square brackets.

Let's illustrate the technique with an example. Consider the linear system

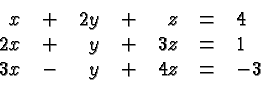
\begin{displaymath} \begin{array}{rcrcrcl} x&+&2y&+&z&=&4\\ 2x&+&y&+&3z&=&1\\ 3x&-&y&+&4z&=&-3\\ \end{array} \end{displaymath}

The system and its processing are described in the following table:


\begin{displaymath} \begin{array}{lrrrrr} \hbox{equation}&x&y&z&\hbox{RHS}&\hbox... ...0&-7&1&-15&-21\\ {[6]=[5]-[4]}&0&-4&0&-8&-12\\ \end{array} \end{displaymath}


Equations $ [1] $, $ [2] $, and $ [3] $ form the original system, augmented by the row sum (RS). RHS stands for the awkward phrase right hand side. (You could also write the right hand side on the left, or you could arrange your equations in columns and write the right hand sides on top or at the bottom, or a separate sheet of paper, if you like.)

Equation $ [4] $ is obtained by subtracting twice the first equation from the second equation. You should check that you get indeed the equation described in row $ [4] $ of the above table. Fully written out it means

$\displaystyle 0x -3y + z = -7. $

Of course we would normally omit the $ x $ term and think of it as

$\displaystyle -3y + z = -7. $

The sum of the coefficients and RHS in that row is

$\displaystyle RS = -3 + 1 -7 = -9. $

The key to the effectiveness of the error detection is that this sum is computed in two ways: actually adding the entries in row $ [4] $, and also by applying to the preceding row sums the same operation as to the equations. In this case we get that the row sum in row $ [4] $ equals the row sum in row $ [2] $ minus twice the row sum in row $ [1] $:

$\displaystyle -9 = 7 - 2\times 8. $

This is the key to many error checking techniques: compute the same thing twice and if you make a mistake in one of your computations it will show up as discrepancy in your two answers.

Row $ [5] $ is obtained similarly, it equals row $ [3] $ minus three times row $ [1] $. The whole purpose of the exercise is that rows (or equations) $ [4] $ and $ [5] $ contain only two variables, namely $ y $ and $ z $. The new system is

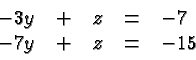
\begin{displaymath} \begin{array}{rcrcl} -3y&+&z&=&-9\\ -7y&+&z&=&-21\\ \end{array} \end{displaymath}

These two equations have the same coefficient of $ z $ (i.e., $ 1 $). If we subtract the second from the first, or in terms of the overall system, row $ [5] $ from row $ [4] $ we obtain the new equation

$\displaystyle -4y = -8. $

This is row $ [6] $ in the above table. It tells us that

$\displaystyle y=2. $

The table does not describe how we find $ x $ and $ z $. Knowing $ y $ we find an equation, e.g., $ [5] $ that contains $ z $ and $ y $. That equation becomes

$\displaystyle -7\times 2 + z = -15 $

which has the solution

$\displaystyle z=-1. $

Finally, substituting $ y $ and $ z $ in the first equation gives

$\displaystyle x+2 \times 2 -1 = 4 $

which implies that

$\displaystyle x=1. $

Checking these results by substituting in the original equations completes the solution of our system.

Notes