MDS User's Guide
Version 157, November 21 2021.
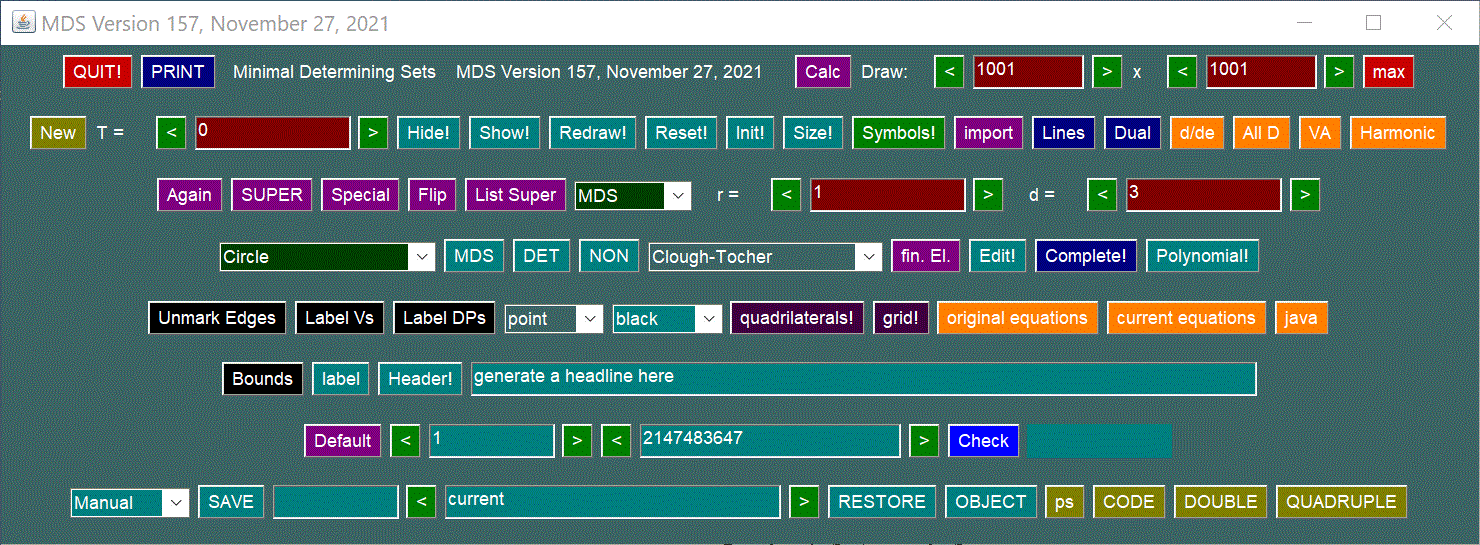
To understand what the applet does you need to understand
the
Bernstein-Bézier form
of a polynomial and the concepts of
spline spaces and their minimal determining sets
.
The Drawing and Analysis Modes
The main use of the applet is to analyze minimal determining
sets. In the first few incarnations of this code that
constituted the only possible use of the software. However,
during the Spring Semester of 1999 my numerical graduate
class persuaded me to add a variation of the Analysis mode
that can be run as a two player game that's quite difficult
and sophisticated and that I hope you will enjoy. It's
described
below
at the end of this User's Guide. There is also a
drawing mode
described below which can be used to label domain points in
various ways (without any analysis done by the code).
The Analysis Mode
As an illustration, the Figure nearby shows the
Clough-Tocher Split, a set of three triangles that
share an interior vertex. The partial minimal determining
set shown is for the case that r=1 and d=6.
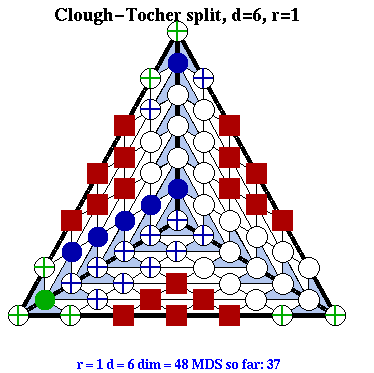 Crosses in circles indicate points in the minimal
determining set, filled colored circles indicate points that
have been determined, and white circles indicate points
whose status has not yet been determined. Boxes indicate
points that do not enter any smoothness conditions. Other
symbols may be substituted in the
drawing mode.
Crosses in circles indicate points in the minimal
determining set, filled colored circles indicate points that
have been determined, and white circles indicate points
whose status has not yet been determined. Boxes indicate
points that do not enter any smoothness conditions. Other
symbols may be substituted in the
drawing mode.
Activating the Software.
Click in the box on the top of this page (or download the
byte code and run it
standalone,
see below).
Two windows will pop up, the control panel, and a
drawing window. The initial triangulation consist of
three triangles sharing an interior vertex (the
Clough-Tocher split). If for some reason you can't get the
applet to work click here for a static image of the
control panel
and here for
an image of the initial drawing window.
(The eighth row of the control panel will not show up if you
are using the applet rather than a standalone version of the
code. This is because Java will not let the applet write on
your machine, and I won't let it write on my
machine. See below for information on how to save your
work.)
If you click on the above applet to make the control panel
and drawing windows disappear you can recover them in the
state you dismissed them by clicking on the applet again,
but only in the same browser section!
You can also
download the byte file and run the program standalone.
On a Unix system you'd invoke the program with the command
java MDS. On my system the program is more
responsive in that mode, I can run it with a specified
amount of memory, it handles
memory problems
more gracefully, and I can
save my work.
.
Quitting.
To quit click on the upper left button (labeled Quit) of the
control panel, or type 'x' in any drawing window.
The polynomial degree and the degree of smoothness.
You can change the values of r (the degree of
smoothness) and d (the polynomial degree)in the
third row of the control panel. There is one red textfield
for r and one for d. To edit any text
field move the cursor into the textfield and click (always
the left mouse button) or highlight part of the text. Then
type the insertion or replacement string. A change in any
text window becomes effective only after you hit Enter
(or Return) on you keyboard. The contents of the
textfields can also be incremented or decremented (by 1) by
clicking on the ">" and "<"
buttons next to the textfield.
Constructing a Minimal Determining Set.
Suppose you want to construct a minimal determining set.
You do this in stages adding one or more points at a time.
Let's refer to the points you have already selected as
the current set. The current set is always a subset of a
minimal determining set, and eventually it becomes equal to
one. To add a point to the current set just click on the
domain point. The first time you do this some linear
algebra will be initialized and any points that do not enter
the smoothness conditions are added. The symbols you see
have the following meaning:
-
a plus sign in a circle: The point is in the current
set.
-
a white outlined circle: The status of that point is as
yet undetermined.
-
a filled in circle: That point is implied to be zero by
the smoothness conditions, based on the points that are
in the current set.
-
a filled in box: That point does not enter any
smoothness conditions and is therefore in any minimal
determining set. It's also in the current set.
-
an outlined white box: That point does not enter any
smoothness conditions and is not included in the current
set, because the linear algebra has not been
initialized, or it has been taken out for some counting
or marking purposes.
Points in the current set can also be taken out, by clicking
on them. Any points that are implied by the larger set, but
not by the smaller, revert to their outlined status.
Adding and removing points in groups.
The menu in the fifth row of the control panel can be used
to determine the effect of clicking on a point, according to
the following options:
-
point. (the default) Add or remove one point at a
time.
-
edge. Select an edge by clicking on any domain
point in its interior. Then add or remove in lines
parallel to that edge by clicking on a domain point in
the interior of the line farthest from the edge. (At
present this works only in the MDS mode, not in the
drawing mode.)
-
ring. Add or remove all points in the ring
containing the target point. To pick the center of the
ring click on that vertex first (in ring mode). The
default center for the predefined vertex stars is the
interior point.
-
disk. This works similarly to the ring option.
-
triangle. Click on an interior point of a
triangle to add or remove the entire triangle, or the
interior point of an edge to add or remove that edge, or
a vertex to add or remove that vertex.
-
All. Clicking on an as yet unmarked point causes
the current set to be completed to form the internal
minimal determining set. This is equivalent to clicking
on the Complete button. Clicking on any other point
causes the current set to be replaced by the empty set.
Thus one can start over without reinitializing the
linear algebra.
-
Replace This is effective only in the
Draw Mode
,
see below. Since it is just too frustrating to be
clicking on points and wondering why this has no effect,
in the MDS mode this option works like the "point
" mode has been selected.
NOTE: Remember to switch back to point mode when done
with one of the other modes. You can do this by using the menu
on the control panel or simply by typing a period in the drawing
window.
Adding Color
The current color can be changed using the second menu in
the fifth row of the control panel. The default is black.
Resizing the Drawing Window
By default, the drawing window is 601 by 601 pixels. There
are three ways to get drawing windows of different sizes:
-
At the beginning of the session by typing java MDS m
n to get drawing windows of size m by n pixels.
-
Resizing a particular drawing window using the standard
system on your computer. This change will effect only
that particular window. The locations of the vertices
will be rescaled. This may change the geometry of your
triangulation. You can, however, select or import new
triangulations in that window which will then be drawn
with the intended geometry.
-
Using the buttons and text fields in the top row of the
control panel. Any such change will apply to subsequent
drawing windows, and the current configuration will be
redrawn from scratch. Width and height can be changed
in steps of 100 pixels, precise dimensions can be
entered in the text fields, and the max button will
cause the window to have the maximum size available on
your computer.
Having more than one drawing window.
You can have several drawing windows at once. The control
window always corresponds to one particular drawing window.
The drawing windows are numbered. You pick which one is
currently associated with the control window by changing the
number in the text field in the second row of the control
panel, the one preceded by the string "T =". You
can increase or decrease that number by clicking ">
" or "< " on the buttons next to it. You
can also edit the contents of the text window. The most
convenient way of associating the control panel with a given
triangulation is to type "c " or "C" in
the relevant drawing window.
Editing a Triangulation
A rudimentary editing facility is available. Clicking on
the button labeled Edit in the fourth row of the
Control Window
brings up an
Editing Window.
At the same time the current triangulation changes into a
simple line drawing with the vertices being labeled.
The coordinates of individual points can be changed using
the textfields in the second row of the Editing Window.
In the third row the indices of three points can be chosen.
Clicking on the button Align will change the
coordinates of the third point P to move it close
to being in one line with the first two points P1
and P2. The program first moves P to the pixel
closest to the projection of P onto the line L
through the first two points. It then searches the
neighborhood of that pixel for a pixel that is actually on
L. It avoids making points coincide. The search
may be unsuccessful, for example if P is in between
P1 and P2 and the differences of the x
and y coordinates of P1 and P2
are two distinct prime numbers. You may be able to
make the alignment possible by changing slightly the
coordinates of P1 or P2 first. Pairs of
parallel edges sharing a vertex are drawn in red.
The Buttons in the top row do the following:
-
Hide finishes the editing process and hides the
editing window. (It can be recalled by clicking the
button Edit on the Control Window.)
-
Redraw Redraws the current triangulation and
puts it into edit mode.
-
Undo Undoes the latest change. This can be
repeated.
-
Finish Puts the current triangulation back into
MDS mode.
The three experimental buttons in the bottom row do the following:
- ReEmbed reassigns the vertex coordinates so that the boundary vertices of the current triangulation lie on a circle. The interior points are rearranged accordingly.
- Shell computes an ordering of the triangles that correspond to shelling the triangulation, starting with an innermost triangle. The list is printed to standard output. The software also recomputes the coordinates of the vertices, but triangles in the corresponding triangulation may overlap.
-
expand degenerate triangles Finds the triangle with the smallest area and moves one of its vertices towards the centroid of a neighboring triangles. The original purpose of this facility was to change degenerate triangles (with zero area) to non-degenerate triangles.
Removing Triangles
It is possible to modify a triangulation by removing a triangle, one at a time. To do so select Remove in the mode menu in the third row of the control panel. To remove a triangle click on an interior domain point of the triangle you want to remove. The software will create a new drawing window with the reduced triangulation. The mode will automatically change back to MDS, to remove another triangle you need to select Remove again int he Mode Menu. The software is based on the assumption that the underlying collection of triangles is shellable. Removing a triangle may create a collection of triangles that cannot be analyzed properly, and that causes the software to crash.
Enumerating Triangulations.
This mode lets you enumerate triangulations with certain
attributes and study their properties. It can be invoked
from the menu in the fourth row.
Much more information can be found here.
Triangular Finite Elements
This mode allows the design of triangular finite elements.
Much more information can be found here.
Miscellaneous Options
The following is a list of options available on the control
panel. not yet discussed:
-
First Row: Pressing on the button labeled "
Calc. " in the upper right corner of the control
panel invokes (or hides) the
Srd Calculator
which is described below.
-
Second Row:
-
New. Clicking on this button brings up a
new drawing window, with the parameters set to
the same value as they are in the current
drawing window.
-
Hide! Hides the drawing window currently
associated with the control panel.
-
Show! Opens the drawing window currently
associated with the control panel, and puts it
on top of all others.
-
Redraw! Redraws the contents of the
current drawing window.
-
Reset! Resets the contents of the current
drawing window. The triangulation and the
values of r and d remain
unchanged. Starting a new MDS requires
reinitialization of the linear algebra.
-
Init! Resets the contents of the current
drawing window and initializes the linear
algebra, without starting the construction of a
MDS. The triangulation and the values of r
and d remain unchanged.
-
Size! Resizes the current drawing window
such that the current triangulation just fits.
This is particularly useful for the custom
drawing mode.
-
Lines Causes an analysis of the set of
all lines connecting pairs of vertices
(segments). Writes the following information to
standard output: Equations for all segments,
lists of segments lying in the same line, lists
of parallel segments, and list of points where
more than two segments intersect.
-
Selecting the
Dual option in the mode menu in the third row of the
control panel
causes a drawing of the dual triangulation.
In the dual a point (a/c,b/c) is written as
[a,b,c] and the line Ax+By+C = 0 is written as
[A,B,C].
The dual is obtained by replacing a vertex [x,y] with the
line [x,y,1].
The line through two vertices is written as
[a,b,c] and mapped to the
point [a,b,c] in the dual. Thus vertices are
mapped to lines, edges are mapped to vertices,
and triangles are mapped to triangles. In the dual
of the triangulation a point is never
shared by more than two triangles, triangles may
overlap, and an edge may be shared by more than
two triangles. The process is its own inverse.
The precise geometry of the dual depends on the
location of the origin, which can be shifted.
Clicking on the original triangulation creates a
new dual drawing with the origin shifted to the
point at which you clicked. The dual mode can
also be invoked by choosing DUAL on the mode menu.
Clicking on a dual window toggles the
labeling of vertices and triangles. Clicking and then
typing x or X closes the dual window.
-
Third Row. The first item in the third row lets
you choose the Analysis Mode (the default) or the
Drawing Mode
described below. Otherwise the third row is dedicated
to the control of r and d.
-
Fourth Row:
-
Symbols The first menu in this row lets
you choose the symbol to be used for drawing in
the drawing mode.
-
MDS. Assigns the currently chosen color
to all points in the current set.
-
DET Assigns the currently chosen color to
all points determined by the smoothness
conditions.
-
NON Assigns the currently chosen color to
all points not entering any smoothness
conditions (those marked with square boxes).
-
The menu in the fourth row provides a choice of
built-in triangulations. These can also be
chosen by hitting the function keys indicated in
parentheses.
-
Custom Triangulation
(see below)
(F1)
-
a single triangle (F2)
-
two neighboring triangles (F3)
-
The Clough-Tocher split (the default)
(F4)
-
a singular vertex (F5)
-
a generic 4 star (F6)
-
a generic 5 star (F7)
-
a defective hexagon (F8). "
Defective " means that the interior
edges of this hexagon from three
parallel pairs. This cause degenerate
dimensions, but the vertex is in fact
confinable.
-
A regular hexagon in the traditional
sense (F9). This vertex is not
confinable.
-
a generic hexagon (F10)
-
the symmetric Morgan-Scott split. (F11)
-
the generic Morgan-Scott split. (F12)
-
Wang's Morgan-Scott split. (F12)
-
Diener's Morgan-Scott split. (
Instability in the dimension of spaces
of bivariate piecewise polynomials of
degree 2r and smoothness order r.
SIMA J. Numer. Anal., 27 (1990), pp.
543-551)
-
Two adjacent Clough-Tocher splits
-
The symmetric double Clough-Tocher Split
-
The generic double Clough-Tocher Split
-
The symmetric Powell-Sabin 6 Split
-
The generic Powell-Sabin 6 Split
-
The (symmetric) Powell-Sabin 12 Split
-
Tannin's Example
-
Yuan-Stillman's Example.
-
Singular version of Yuan-Stillman's example
-
extended Yuan-Stillman's example
-
triple Yuan-Stillman
-
4 complex, a ring surrounding a singular vertex
-
generic 4 complex, a ring surrounding a 4-star
-
6-complex, a ring surrounding a regular hexagon
double 6-complex, a double ring surrounding a regular hexagon
-
triple 6-complex, a double ring surrounding a regular hexagon
-
The 1-split, a 4-cell with each triangle
split by Clough-Tocher
-
Cells or Vertex Stars. This
brings up a
separate control window
which lets you construct a cell or
vertex star, i.e., a triangulation with
one interior vertex and no flaps. E
is the number of boundary vertices
(and interior edges) and e is
the number of distinct slopes assumed by
the interior edges. You can also make
one or more edges degenerate at a
boundary vertex (i.e., make the two
boundary edges emanating from the vertex
parallel) by entering the index of the
boundary vertex in the textfield
provided.
-
Regular Triangulations. This
brings up a
separate control window
which lets you investigate spline spaces
on regular triangulations. These are
obtained by starting a rectangular net
and drawing in one set of diagonals
(giving a type-I triangulation) or
drawing in both sets of diagonals
(giving a type-II triangulation). The
regular versions as well as generic
versions (where no vertex has a pair of
parallel edges attached) are available.
Computations take a long time for large
triangulations and can be triggered
manually, after all settings are right,
or automatically, after each change.
-
Enumerate. Selecting the item has
the same effect as pressing the
Enumerate Button. The mode is
described here.
-
Complete Constructs a complete minimal
determining set starting with those points that
have already been chosen.
-
Fifth Row:
-
(Un)Mark Edges Toggle, causes parallel
pairs of edges sharing a vertex to be drawn in
red.
-
Label Vs Toggle, shows or hides the
internal numbering of the vertices. Interior
vertices can be omitted or included by typing
l.
-
Label BPs Toggle, shows or hides the
internal numbering of the Domain Points
-
quadrilaterals toggles the drawing of the
quadrilaterals symbolizing the smoothness
conditions.
-
grid toggles the grind in each triangle
on and off.
-
Sixth Row
-
label
Turns a label at the bottom of the drawing
window on or off. That label contains a count
of the points in the current set, and a
statement of the dimension of the spline space.
The label is active only after the linear
algebra is initialized. When present it changes
whenever the current set changes.
-
Header Turns a headline in the drawing
window on or off. The text of that headline can
be chosen in the textfield next to the button.
Seventh Row The applet uses
residual integer arithmetic
modulo one or more
prime numbers.
Ordinarily you will not need to use the controls in the
seventh row. However, you may be interested in
a fascinating topic, or you may have a crucial
application. So here is a brief description of the
functions of the items in this row:
-
The Default button establishes these
defaults: use one prime only, and let it be the
largest prime that can be expressed as an
integer in Java, i.e.,
p = 2 31 -1 = 2,147,483,647
-
The first text field with its decrement and
increment buttons sets the number of primes
being used. The minimum (and the default) is 1,
and the maximum is determined by the memory of
your machine. The time the program takes for
its analysis is roughly proportional to the
number of prime numbers being used, and 1
(large) prime number is enough for almost all
purposes.
-
The second text window contains the largest
prime being used. It should almost always equal
the default value. However, you can reduce it
to see how the applet works with smaller prime
numbers. If you enter a composite number it
will be replaced by the next smaller prime
number. Numbers less than 2 are replaced by 2.
The familiar green buttons allow easy increments
and decrements of the current top prime number.
-
The Check button initiates a check of the
residual that so far have been computed. The
check requires that at least two prime numbers
be used, and it is carried out automatically at
the end of the
initialization phase.
The results of the check are indicated at the
label next to the check button.
-
The label at the end of the seventh row
indicates the status of the residual arithmetic.
There are these possibilities:
-
The Label is white if no statement can
be made. This is the case when only one
prime number is being used or the linear
algebra has not yet been initialized.
-
The Label is green with a statement
PRIMES OK. This means the
residuals in all
matrix entries
are either all zero or all non-zero.
-
The label is red and shows three
numbers like
2 15 29
This means the
system matrix
contains 29 non-zero entries, 15 of
which have some zero residuals. The
maximum number of zero residuals is
2. If a situation like this occurs
the background of the drawing window
changes from white to pink. In the
unlikely case that this happens with
the default top prime (2 31
-1) I'd like to hear from
you!
.
So far to my knowledge this event has
never occurred!
The situation is illustrated for
small prime numbers in this screen
image
(which also shows what part of my screen
looked like during the development of
this applet and these pages.
Eighth Row The eight row is present only in
standalone mode
.
It contains controls for
saving and restoring your work.
Progress Indicators
During certain time consuming process the drawing window
indicates what's happening. The word Initializing is
present during the initialization of the
linear algebra
,
and a moving colored bar indicates progress. In particular
the bars indicate:
-
Red
on
Cyan
: The smoothness conditions are being set up.
-
Yellow
on
Red
: The linear system is being reduced to
triangular form.
-
Green
on
Yellow
: The linear system is being reduced to
diagonal form.
-
Blue
on
Magenta
: The system is checking for
zero residuals
.
Keyboard Commands
Several Keyboard commands are available in each drawing window.
The list below will be extended in the near future. The idea is
that essentially one should be able to control each drawing
window without using the control panel at all.
|
D
|
increment d by 1
|
|
d
|
decrement d by 1
|
|
R
|
increment r by 1
|
|
r
|
decrement r by 1
|
|
0
|
make current color
black
(the default)
|
|
1
|
make current color
red
|
|
2
|
make current color
green
|
|
3
|
make current color
blue
|
|
4
|
make current color
cyan
|
|
5
|
make current color
magenta
|
|
6
|
make current color
yellow
|
|
7
|
make current color
White
Note: use this color with caution and only for
special effects because the background of the
drawing is white and the interior of circle and
square outlines is also white.
|
|
RETURN
|
redraw the net
|
|
o,O
|
restart
|
|
p
|
Turn position indication during Custom Design
OFF
|
|
P
|
Turn position indication during Custom Design
ON
|
|
q,Q
|
hide window
|
|
x,X
|
exit system
|
|
c,C
|
associate the control panel with this window and
put it on top
|
|
.
|
point mode
|
|
/
|
edge mode
|
|
@
|
ring mode
|
|
#
|
disk mode
|
|
$
|
triangle mode
|
|
all mode
|
all mode
|
|
F1-F12
|
choose a triangulation (see above)
|
|
l
|
label the vertices, toggle between omitting and
including boundary vertices
|
|
S
|
Enter
Super spline
mode.
|
|
I
|
Initialize MDS computation.
|
|
m or M
|
List the current set to standard output.
|
|
u or U
|
Undo the previous step in designing a custom
triangulation. This can be repeated. Can also
be used to undo the last step taken in the
drawing mode, but in that case the command can
be used only once.
|
|
z
|
Toggle the listing in the drawing window of the
indices of the domain point that the cursor is
currently pointing to. This feature is useful
when working with b-nets of very many domains
that are close together. The default is off.
This is an experimental feature. The display
sometimes gets confused, and can be restored by
redrawing the net, e.g., by hitting the return
key.
|
|
< and >
|
Decrease or increase the current symbol Size.
|
If the keyboard command is not recognized a message is sent to
standard output.
Text Output
At present, textual information (to standard output) is very
sparse. When a triangulation is completed it is described. The
dimensions and rank of the original matrix is stated and a list
of the prime numbers used is given.
For example, the default Clough-Tocher split with r=1
and d=3 causes this description:
MDS: MDS Version 148, May 2020
New Triangulation
4 Vertices
0: (591,180)
1: (225,858)
2: (771,780)
3: (529,606)
3 Triangles:
0: 0 2 3
1: 1 2 3
2: 0 1 3
3 boundary edges:
0: 0 2
1: 1 2
2: 0 1
3 interior edges:
0: 2 3 --- 0 1
1: 0 3 --- 2 1
2: 1 3 --- 2 0
3 boundary vertices: 0 1 2
1 interior vertices: 3
19 Bezier Points
lb = 12 ub = 12
Most of this information is readily understood taking into
account the fact that the interior vertex of the Clough-Tocher
split is vertex 0. The vertices coincide with specific pixels
whose coordinates are integers, with the origin in the upper
left corner, x increasing to the right, and y increasing
downwards. An interior edge is described by the pair of indices
of its vertices, and the indices of the remaining vertices of
the attached triangles. For example, "0 1 --- 3 2"
means the interior edge is the edge shared by the triangles (0,
1, 3) and (0,1,2).
For each interior vertex v, E is the number of
edges attached to v, and e is the number of
different slopes these edges have. For example, the four edges
emanating from a singular vertex form two parallel pairs, so
E=4 and e=2.
The
lower bound
given is known to equal the exact dimension of the spline space
whenever d>3r+1.
Typing "s" (for statistics) in the drawing window
causes information like this (obtained after clicking on "
complete" in the default setup) to be displayed:
checking ...
7 equations 12 active variables
equations OK ...
fill = 29/84 (34%)
total of 597 Residuals
The likelihood of no accidentally zero residuals is 99.999%
This means the reduced system has 7 equations in 23 active
variables. 29 entries in that matrix are non-zero. The phrase
"equations OK" is a leftover from the debugging days -
it means the coefficients in each equation add to zero. They
must since the function that equals 1 everywhere is a spline all
of whose Bézier coefficients are 1. Please let me know
it you ever get a message that the equations are not OK! The
"total number of residuals" is the number of times a
residual was computed since the last initialization of the
linear algebra.
The word "fill" indicates the number of non-zero
entries in the matrix compared to the total number of entries.
In the above example a total number of 597 residual has been
computed so far. (That number can easily climb into the
millions.)
When only one prime number is used the likelihood that none of
the computed residuals of non-zero matrix entries is zero is
displayed. This is based on the assumption that all residuals
are equally likely. The likelihood is usually close to 100% if
the default prime of 2 31 -1 is used. You may find
it interesting to examine this likelihood for small prime
numbers. When several prime numbers are used the likelihood of
an accidentally zero residual actually increases, but the
likelihood of a correct minimal determining set increases, so
the likelihood statement is omitted. For more information
check the page on residual arithmetic.
The Srd Calculator
Dimensions and
lower bounds on the dimension
can be computed by using the
Srd Calculator.
The calculator does not require analysis of a linear system,
saving a potentially large amount of time, and you may find it
interesting to compare the lower bound with the actual dimension
of your spline space.
It is a separate window that can be invoked by clicking on the
button in the upper right corner of the control panel.
Essentially it computes a lower bound on the dimension of the
current triangulation of the form
dim S <= A V B + B V I C + sigma
(*)
which is
explained here.
The bound equals the true dimension whenever
d > 3r+1
and in many other situations also. It becomes less reliable as
the polynomial degree decreases.
When the calculator is brought up it shows the lower bound (*)
for the current triangulation and the current values of r
and d. The lower bound is displayed in the lower
right corner of the calculator window. Usually That expression
gets updated automatically whenever the triangulation (or r
or d ) changes. However, the values of r
, d, V B , and V I
can be changed on the calculator panel itself, and
the values of A, B and C will change
accordingly.
This facility is most useful for examining the dependence of
A, B, and C on r and d.
It is less useful to change V B and
V I since the resulting value of the lower
bound does not apply to any particular triangulation.
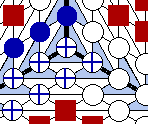
A little more subtle is the value of e V
that can be changed in the right most text field in row 2. If
it is white with no text in it it has no effect on the number in
the third row of the panel. However, if you enter a number then
the number sigma in the third row will equal
You may find it interesting to study the dependence of
sigma on r, d, and e V
, but the lower bound in the fourth row will have a very
arcane meaning.
The Hide button hides the calculator window. (You can
recover it by pressing on the Calc. button in the control
window.) The Get button synchronizes the calculator with
the current triangulation (the one associated with the control
panel).
Every update of the calculator also causes an appropriate line
of text to be written.
Designing a Custom Triangulation
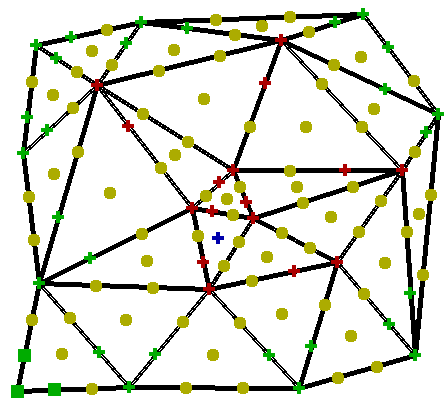 The image nearby shows the domain points for C 1
cubic on a custom designed triangulation. The dimension
of this space in general is believed to be 3V B +
2V I + 1 plus the number of singular vertices.
The example shows 3 domain points associated with each boundary
vertex, 2 with each interior vertex, and one additional point
(the lone blue plus sign in the center of one of the interior
triangles).
The image nearby shows the domain points for C 1
cubic on a custom designed triangulation. The dimension
of this space in general is believed to be 3V B +
2V I + 1 plus the number of singular vertices.
The example shows 3 domain points associated with each boundary
vertex, 2 with each interior vertex, and one additional point
(the lone blue plus sign in the center of one of the interior
triangles).
You can design your own triangulation by selecting the three
vertices of the first triangle and then adding flaps
(new triangles joined to the old triangulation along one edge)
and fills (new triangles joined along two edges).
Follow these steps:
-
Select custom mode by using the menu on the control panel or
by typing F1.
-
Draw the first triangle by moving the mouse to the intended
locations of the vertices and clicking there. To facilitate
precision, once you have placed the first vertex the
coordinates of the mouse position relative to the first
vertex will appear in the drawing window. You can turn this
option off by typing p (for position) and turn it
back on by typing P.
-
Add flaps by moving the mouse to the midpoint of the
newly to be interior edge and dragging the mouse to the
intended location of the new boundary vertex. Once you let
go of the mouse button that vertex cannot be moved. The
location of the new vertex is indicated as described above.
-
Add a fill by clicking on the newly to be interior
vertex.
-
If you do not like the triangle you just added type "u
" to undo your choice. If necessary this
process can be repeated until all triangles are gone. You
can also abort adding a flap by moving the mouse outside the
drawing window.
-
When you are finished with your triangulation type "f
" or "F" in the drawing window. You can now
use this triangulation like any of the others.
-
To return to the design mode click on the button labeled
"Again" in the control panel.
Importing a Triangulation
Pressing the button labeled "import" opens a new
window that lets you load a triangulation from a file (only in
stand-alone mode) or a URL. The file needs to contain the
following data: V and N on the first line, followed by V lines
containing the coordinates of the points, one point per line,
followed by N lines containing the indices of the vertices of
each triangle, one triangle per line. The integers must be
separated by blanks, and the lines must not contain other data.
For example, the file for the CT split would be:
4 3
302 88
80 514
521 514
301 372
2 0 3
2 3 1
3 0 1
The Save Button saves such files with the extension .cmb
The Drawing Mode
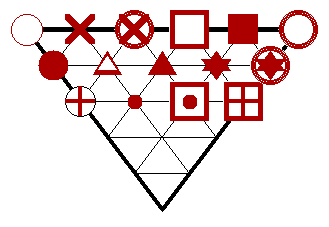
The drawing mode is invoked with the menu in the third row. You
can first do some analysis in the analysis mode and then switch
to the drawing mode to change some of the symbols. However, if
you switch from drawing mode to analysis mode then the drawing
window gets reinitialized, so beware!
Several symbols can be used. They are selected by the menu in
the fourth row and illustrated in the Figure nearby. Everything
on the control panel works as in the Analysis mode when it makes
sense. (For example, it does not make sense to ask the applet
to color all the points in the minimal determining set.)
In the single point mode (selected by the first menu in the
fifth row) clicking on a point that has already been labeled
with the currently selected symbol causes that symbol to be
replaced with a circle. (This is like removing a point.) In the
ring, disk, and triangle modes points are marked with the
selected symbol regardless of their prior status. In the "
all" mode all points as yet unmarked (indicated by single
thickness circles) are marked with the currently selected
symbol. In the "replace" mode all points marked as
the selected point are marked with the selected symbol. Changes
made in any but the point mode can be undone by typing "u
".
Normally the size of the symbols drawn in the drawing window is
determined automatically and depends on the current density of
domain points. However, it can be set manually for special
purposes. Click on the button labeled Symbols (in the
second row of the main control window). A new window, the
size control window, appears. The symbol size (in pixels)
is displayed in its text field. It can be changed with the two
arrow buttons or by entering a new size in the text field.
Clicking on "Default" in the size control window
replaces the symbol size with its usual automatically computed
value. Clicking on automatic in the size control window,
or again on Symbols in the main control window, causes
the size control window to disappear and symbol size control to
revert to automatic. While manual control is in effect the
symbol size will not change if the density of the domain point
changes, for example in response to changing the value of d
or picking a new configuration. The current triangulation
is redrawn whenever the current value of its symbol size is
changed manually.
Saving Your Work
It is possible to save your work, but for security reasons
Java will not let my applet write on your
machine (and I won't let you write on my
machine). You need to download the byte code as described
in the next section. If you run that code (directly rather
than via a browser) on your system there will be an eighth
row on the control panel (shown on
on this static image)
which lets you specify a file name and read and write to
that filename.
The individual items in the 8-th row do the following:
Notes: Any restoration takes place in a new drawing
window. Thus you can explore different branches using the
Object button, or retract your steps without loosing your
work using the Restore button.
Saving High Resolution Postscript Images
Pressing the button
ps
on the control panel brings up a new panel that lets you
save the contents of the drawing window as a high resolution
postscript image. The text field on the postscript panel
lets you specify a file name, the
save
button actually saves the file, and the
ColorMode
button toggles between full color mode and gray scale (which
may be required by some publishers). The menu on the
postscript panel lets you specify several image sizes and
aspect ratios, as follows:
-
full letter (default). The image is scaled
to fill US letter size (8.5 by 11 inches)
completely.
-
screen letter. The aspect ratio of the
drawing window is preserved, but otherwise as much
space as possible is used on letter size paper.
-
screen. The screen size is used, with one
pixel corresponding to 1 point (and 72 points
corresponding to one inch). Thus very small or very
large images independent can be obtained independent
of the paper size.
-
square letter. As large a square as possible
(8.5 by 8.5 inches) on letter paper is filled.
-
legal. US legal paper (8.5 by 11 inches) is
filled.
-
11x17. 11 by 17 inches are filled.
-
17x22. 17 by 22 (four letter sheets) inches
are filled.
-
A4. European A4 (210 by 297 millimeters) is
filled.
Interfacing with Other Codes
The buttons labeled "CODE", "DOUBLE
", and "QUADRUPLE", in the bottom row of
the control panel computes data in floating point form
and save them to a file s.code where s is the
string determined by the other items in this row. Saving
the "CODE", information can also be invoked by
typing w or W in the drawing window.
The bars in the drawing window in turn show progress in
setting up the floating point equations, reducing the
system to triangular form, and then reducing it to
diagonal form. The primary contents of the s.code is
the matrix C where
d = Cc,
c is the vector of coefficients whose domain
points are in the minimal determining set and d
is the vector of coefficients that's determined by the
smoothness conditions.
The files s.code differ in subtle ways. Click on the
links below to see the file for the cubic C 1
CT scheme.
-
"CODE"
:
These data are computed using ordinary floating
point arithmetic.
-
"DOUBLE"
:
For these data the MDS code internally uses
arbitrary precision rational arithmetic. The
entries of C are printed as floating point
numbers that are precise to 16 digits. They are
also given as exact rational numbers. Computing
this information takes much longer than computing
the "CODE" version. However, subsequent
computations involving C are likely to be
more accurate.
-
"QUADRUPLE"
:
These data re essentially the same as those obtained
by "DOUBLE", except they are printed to
quadruple precision (32 digits).
The buttons "DOUBLE" and "QUADRUPLE"
also produce a file
s.explicit
which contains an exact rational representation of the
determined coefficients in terms of those corresponding
to the minimal determining set.
Super Splines
Super splines are splines that satisfy
additional smoothness conditions. (They thus form a
subspace of an ordinary spline space.)
To examine a super spline space do the following:
-
Bring up the triangulation you want and set r
and d as usual.
-
Enter Super spline mode by clicking on the red
button marked "Super", on the left in the
third row of the control panel. Or achieve the same
effect by typing S (in the drawing window).
-
To increase smoothness around a vertex click on the
vertex. Each time you click the smoothness
requirements are increased by one. They are
indicated by yellow quadrilaterals.
-
To increase smoothness requirements across an edge
click close to the center of the edge. These
additional conditions are indicated by Cyan
quadrilaterals.
-
You can also increase smoothness requirements by
typing + or decrease them by typing -
. These typed commands apply to the last
object (vertex or edge) selected by clicking.
-
You can also impose additional individual smoothness
conditions which are indicated by magenta
quadrilaterals. To do so proceed as follows:
-
Click on the button labeled "Special
" in the third row.
-
To impose a condition whose quadrilateral is
across the interior of an interior edge
click first in the middle of that edge and
then on a domain point to the side of that
edge.
-
If one of the vertices of the quadrilateral
is a vertex of the triangulation, in other
words, if the quadrilateral is at the end of
an interior edge, first click on that vertex
and then on the appropriate point in the
interior of the edge.
-
Finally, to impose a C d
condition across an edge, double-click on an
interior domain point on that edge.
-
To initiate the MDS analysis of the superspline space click on Init!
in the second row of the control panel, again click
on SUPER, or type I.
-
To modify the supersmoothness conditions return to
superspline mode by clicking on the "Again
" button next to the "Super" button.
Notes:
Once you enter Super spline mode you cannot exit it without
(re-)initializing the linear algebra.
You remain in super spline mode (and maintain the current
additional smoothness conditions) if you change d
or r. However, there is no intelligent
adjustment in the degrees of the additional smoothness
conditions.
Reduced Polynomial Degree
It is possible to impose
additional conditions
that force the splines to have a reduced polynomial
degree on selected triangles. This option is treated
like a superspline condition although it is conceptually
different. To reduce the polynomial degree on a certain
triangle by 1 enter superspline mode and click close to
the center for the triangle. The triangle will be drawn
in green, and the (reduced) polynomial degree will be
drawn in red, close to the center of the triangle. That
red number may be partially obscured by the B-net which
is also drawn. The + and - keys work
as they do for the superspline conditions, +
increase the polynomial degree (up to d ) and
- decreases it. Here are are some
examples
of polynomials with lesser degrees than meets the eye.
Pressing the button labeled Bounds in the sixth
row of the control panel turns the computation of bounds
on and off. The best available current bounds are
displayed at the top of the drawing window. The feature
is on by default. This is an active research topic
under current investigation.
Running Standalone and Downloading the Code
Alternatively, on a Unix system you can download the
single file
message
,
put it into an empty directory, and type source
message. This will unbundle the class files and
bring up the MDS code. Alternatively, you can download
the zip file
MDS.zip
which has all required class files.
Details of how to run the byte code on your machine
depend on your operating system. On my (Unix) machine
the command
java MDS
invokes the program. You need to be connected to the
directory containing the byte code. Type
man java
to obtain information on options you may be able to
specify. For example, on my system the command
java -ms128m -mx128m MDS
will cause the program to run with 128 Mbytes of memory
allocated to it (in place of the default 16Mbytes).
Printing Triangulations
You can save the image of a triangulation to a
postscript file or directly print that image. To do so
click on the Print button in the first row of the
control panel or type Control-P in the drawing window.
This facility works only in the standalone mode. If run
from an applet, a security exception occurs.
Assigning Polynomials
For test purposes (e.g., checking polynomial precisions)
polynomial coefficients can be assigned on one triangle.
The software can the compute the coefficients of the same
polynomial on all other triangles. To use this feature
click on
Polynomial
in the control panel, fill in the coefficients in the new
Polynomial panel, and click on Assign in the
Polynomial Panel. The resulting coefficients will show in
the drawing window.
Examining Derivative Spaces
This facility is currently [June 2012] under development
and does not have all the features associated with the
regular spline spaces.
Let D denote a directional derivative, and S a spline
space being examined by the software. Clicking on the
orange button labeled d/de in the main
control panel brings up a new drawing window and a new
control window that let you examine the space of
functions Ds where s is in S. The drawing window shows
the coefficients of s as usual, and the coefficients of
Ds as triangles. Those triangles are clickable, and
their color indicate their status. Dark blue means they can
be set, light blue they have been set, and gray they are
implied by other coefficients (of s or Ds) that have
been set. The control window let's you pick the
direction of differentiation. It can be chosen as a
linear combination of edges in the triangulation, or as
a vector in 2-space. The coefficients and vertices can
be labeled, and the original equations can be printed.
Clicking on the orange button All D in the main
control window brings up a similar control panel that
lets you examine Bézier nets for all derivatives.
You can pick two directions, again in terms of Cartesian
Coordinates, or as a linear combination of two edges.
These directions are designated x and y
although they can be in any direction.
On both panels the following buttons have these effects:
-
Exit exits and removes all windows related to
derivative spaces.
-
dim? prints dimension statements to standard
output.
-
Reset reinitializes the linear algebra
-
Restart removes all points currently marked
as having been set. Under normal circumstances the
visible effects of Reset and Restart should be
identical.
-
ListEqs labels domain points and derivative
triangles in the drawing windows, and lists the
original equations.
-
Label Vertices toggles the labeling of
vertices.
-
Similarly, Label Variables toggles the
labeling of domain points and derivative triangles.
-
Redraw redraws all drawing windows. You can
redraw an individual drawing window by focusing on
it and hitting the Enter key.
-
Go recomputes the directions and
reinitializes the linear algebra. Use it after
changing the direction(s).
Additional buttons on the All Derivatives panel include:
-
All Show all drawing windows
-
None Hide all drawing windows
-
Show Master One of the drawing windows
serves as the master that does all the calculations.
It is the first drawing window made visible, and it
is distinguished by having a different background
color. Clicking on this button puts the master
window on top of all windows. It shows how many
conditions have been imposed.
-
edges prints a list of edges, including
their cartesian coordinates, to standard output.
-
Individual derivatives buttons (labeled, S,
Sx, etc.) make individual drawing windows
visible or invisible. The buttons are green for
visible windows, and yellow for invisible ones.
Clicking on a green button twice brings the
associated window to the top.
Vector Analysis
This works similarly as single derivative analysis and is
currently under development.
We consider a vector field whose components are two
splines P and Q. The divergence and
curl of the field are defined by
div ( P, Q ) = P x
+ Q y and
curl ( P, Q ) = - P
y + Q x ,
respectively.
Clicking on the Button labeled Vector Analysis in
the control panel brings up a new vector control panel
and a new vector drawing window. They let you analyze
the vector field based on the spline defined in the
current triangulation, including any supersmoothness
conditions. Any change in the current triangulation has
no effect on the vector windows once they are produced.
The original definitions of div and curl
are with respect to the x and y directions
but those can be changed in the first row of the vector
control window. The text fields there can be used to
enter a new direction which replaces the x
direction. The replacement of the y direction is
perpendicular to the new x direction. For
simplicity we well refer to the new directions also as
x and y directions.
The coefficients of the vector components, and those of
div and curl, can be set in the vector
drawing window. The circular domain points there
correspond to the coefficients of P and Q,
and the triangles correspond to the coefficients of
div and curl. Left clicking on a domain
point or a triangle sets P or div,
respectively, and right clicking sets Q or
curl, respectively. Clicking the middle button has
the same effect as first clicking left and then clicking
right. P is represented by blue, Q by
green, div by red, and curl by yellow. A
saturated color indicates that the coefficient is
available, a pastel color that it has been assigned, and
gray indicates that it has been implied.
The controls in the control window have the following
effects:
Harmonic Splines
Clicking on the button labeled "Harmonic" (the last button in the second row of the main control panel) adds equations that make all polynomial pieces harmonic (Laplacian equals zero).
Performance
The following table gives an indication of the
capabilities of the code. The underlying triangulation
is the generic double Clough-Tocher split with d=2r
for r=1,2,...,10. The columns in the
table have the following meaning:
-
r, d the values of r and d
(naturally)
-
m The original number of smoothness
conditions.
-
n The number of domain points involved in
smoothness conditions.
-
rank The rank of the original matrix.
-
dim The dimension of the spline space. In
this case dim = n-rank. If d is
large enough so that there are points not entering
any smoothness conditions one would have to add the
number of those points to obtain the dimension.
-
fill The percentage of points in the reduced
matrix that are non-zero.
-
save The amount of disk space in kiloBytes
taken up by the .obj file storing this
triangulation, after initialization of the linear
algebra.
|
generic double-Clough-Tocher split, d =
2r
|
|
r
|
d
|
m
|
n
|
rank
|
dim
|
fill
|
save
|
|
1
|
2
|
24
|
22
|
16
|
6
|
82%
|
8
|
|
2
|
4
|
84
|
79
|
61
|
18
|
80%
|
28
|
|
3
|
6
|
180
|
172
|
138
|
34
|
79%
|
87
|
|
4
|
8
|
312
|
301
|
244
|
67
|
82%
|
240
|
|
5
|
10
|
480
|
466
|
381
|
85
|
82%
|
504
|
|
6
|
12
|
684
|
667
|
547
|
120
|
86%
|
984
|
|
7
|
14
|
924
|
904
|
745
|
159
|
83%
|
1,728
|
|
8
|
16
|
1,200
|
1,177
|
972
|
205
|
86%
|
2,864
|
|
9
|
18
|
1,512
|
1,486
|
1,231
|
255
|
80%
|
4,464
|
|
10
|
20
|
1,860
|
1,831
|
1,518
|
313
|
76%
|
6,856
|
The MDS Game
The mode menu (the second item in the third row of the
control panel) lets you select a game mode in which you can
construct a MDS taking turns against an opponent who's
trying to determine more points than you.
To explain the rules we need to distinguish between
points you or your opponent add to the current set,
and points that count towards your victory. Let's call
the latter cookies to avoid confusion.
The rules are as follows:
-
You get a cookie for every domain point whose B
é zier ordinate is determined by a point you
add to the current set.
The player ending up with the largest number of
Cookies wins.
-
You and your opponent take turns
-
You turn is over if you get at least one cookie, or
after you add the second point of your move to the
current set. The program indicates whose move it
is.
Notes
-
The reason for not simply alternating adding one
point is that this would give a significant
advantage to the player who is going to add the last
point, since that would turn all remaining points
into cookies. With the above rules, it is not clear
a priori who will make the last move.
-
Points added and cookies gained are marked in red
for the first player, and green for the second.
-
The program also displays the current score, the
final result, and the number of points still to be
added to the current set (so you can plan your
strategy).
-
To avoid confusion, the facilities to remove points,
to change colors, and to add points in groups, are
disabled in the game mode
-
Inactive points play no role in the game, and
therefore are not displayed.
-
The game can of course be played on any
triangulation, and for any values of r and
d. You may also wish to explore playing
with small prime numbers where the usual rules may
not apply due to accidentally zero residuals.
Have fun!
Write to me
Please write to me
if you encounter any bugs or you like to make suggestions
for additional features.

[22-Jun-2012]
 Crosses in circles indicate points in the minimal
determining set, filled colored circles indicate points that
have been determined, and white circles indicate points
whose status has not yet been determined. Boxes indicate
points that do not enter any smoothness conditions. Other
symbols may be substituted in the
drawing mode.
Crosses in circles indicate points in the minimal
determining set, filled colored circles indicate points that
have been determined, and white circles indicate points
whose status has not yet been determined. Boxes indicate
points that do not enter any smoothness conditions. Other
symbols may be substituted in the
drawing mode.


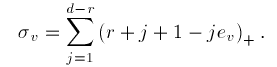
 The image nearby shows the domain points for C 1
cubic on a custom designed triangulation. The dimension
of this space in general is believed to be 3V B +
2V I + 1 plus the number of singular vertices.
The example shows 3 domain points associated with each boundary
vertex, 2 with each interior vertex, and one additional point
(the lone blue plus sign in the center of one of the interior
triangles).
The image nearby shows the domain points for C 1
cubic on a custom designed triangulation. The dimension
of this space in general is believed to be 3V B +
2V I + 1 plus the number of singular vertices.
The example shows 3 domain points associated with each boundary
vertex, 2 with each interior vertex, and one additional point
(the lone blue plus sign in the center of one of the interior
triangles).

