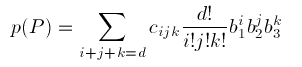
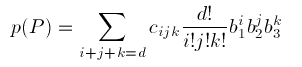
may of course actually be of a degree less than $d$. When it is that fact is not readily apparent in the B-form. However, the MDS code described on these pages allows for the imposition of additional conditions on the coefficients of p that force it to be of a lesser degree than d. These conditions are derived and illustrated on this page.
A polynomial of degree d will be of degree d-1 if d+1 independent derivatives of order d vanish. Similar conditions can be obtained to force p of degree even less than d-1. For simplicity we only described the conditions used to obtain the degree d-1.
The MDS code forces p to satisfy the conditions
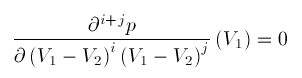
where
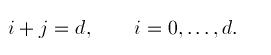
It's easy to see (and discussed elsewhere) that
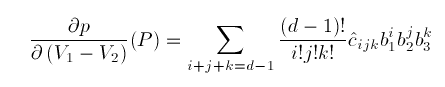
where
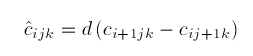
Similarly,
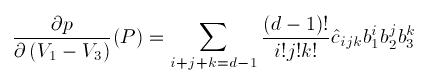
where
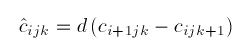
Thus we obtain, for example, that
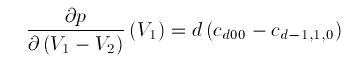
and
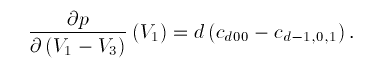
Repeating this process gives rise to the conditions
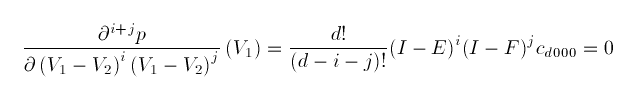
where I is the identity operator and the shift operators E and F are defined by
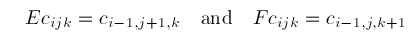
Obviously we can ignore the constant factor in these homogeneous conditions. Since the operators E and F commute we obtain the conditions
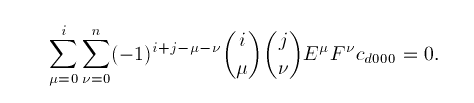 (*)
(*)
where
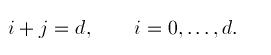
There is just one more subtlety. The coefficients multiplying the Bézier coefficients in these equations are in fact integers. However, because of the binomial coefficients they are defined as rational numbers and I did not see a straightforward way of evaluating them in residual arithmetic. To overcome this problem the MDS code actually implements the conditions (*) multiplied with i!j!. They therefore take the form
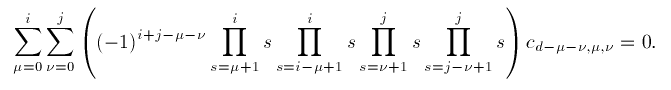
(A similar trick is used for implementing the cross-boundary smoothness conditions.)
Click here to see some examples of reduced polynomial degrees.