

The first example shows the familiar
Clough-Tocher element camouflaged as a spline of degree
4 rather than 3. The points marked in black are
determined by interpolation to function and gradient values at the
vertices of the macrotriangle. The points shown as black circles are
implied, those shown as black cross hairs are given as data.
The three turquoise cross hairs are given by the cross boundary
derivative data, the turquoise solid circles are implied by the
smoothness conditions. The dimension of this spline space is 12. This
contrasts with the dimension of C1 quartics, which
is 21.

A similar element could be built on the generic Morgan-Scott split
,as illustrated in the Figure nearby, by reducing the degree of the
central triangle to 2.
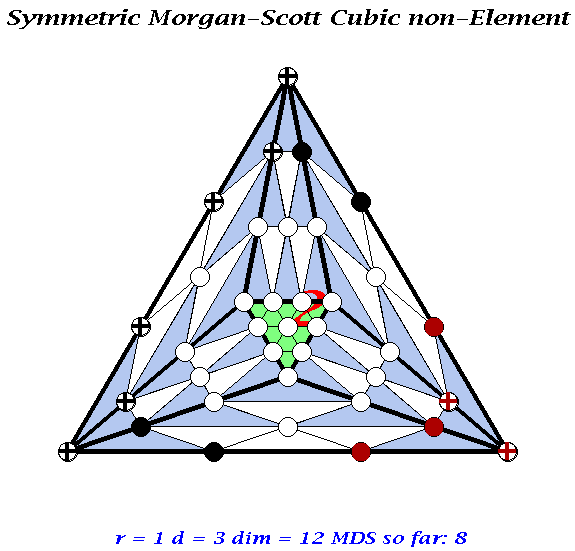
However, it the same idea is applied to the symmetric Morgan-Scott split then it turns out that the vertex data cannot be all imposed, as indicated in the lower right corner of the Figure nearby. Imposing the function value and one directional derivative implies all other directional derivatives.
Of course, the C1 cubic Clough-Tocher element works perfectly fine and there is no need to construct a C1 element on the Morgan-Scott split. However, I've been trying to construct smoother elements on a symmetric split and the phenomenon illustrated here seems to be inevitable: the last piece of data needed on the boundary to ensure smoothness between macrotriangle always seems to be dependent on the other boundary data. This subject is under investigation.