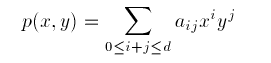 (1)
(1)
A bivariate polynomial p of degree d is a function of the form
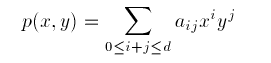 (1)
(1)
where x and y are the independent variables and the aij are the coefficients. i and j are non-negative integer indices.
There are many alternative ways to write p. If the
relevant domain of p is a triangle (as it
is in many applications (like the finite element method or
the design of surfaces) then the Bernstein-Bézier form is
particularly appropriate.
Let's denote the relevant triangle by T. Denote the vertices of T by V1 , V2 and V3. Any point P in the plane can be expressed in terms of barycentric coordinates b1, b2 and b3 defined by
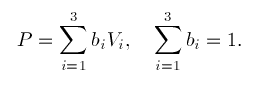 (2)
(2)
The Bernstein-Bézier form of p is given by
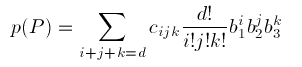 (3)
(3)
The cijk are the Bézier ordinates (or Bézier coefficients) of p and the integers d!/(i!j!k!) are convenient normalizing factors.
Note that the sum of the subscripts i, j, and k is equal rather than less than or equal to d, and that there are as many coefficients in (3) as there are in (1).
It can be easily verified that (3) does indeed define a polynomial of degree d and that any polynomial of the form (1) can be written uniquely in the form (3).
With each Bézier ordinate we associate a domain point
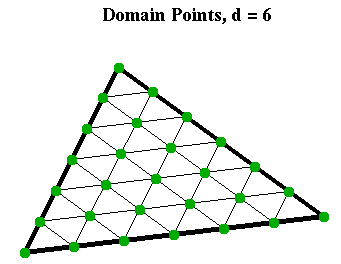
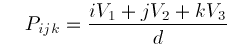 (4)
(4)
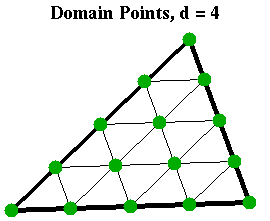
These points form a regular triangular array of (d+2)(d+1)/2 points in the triangle T. They are illustrated for d=4 and d=6 in the Figures nearby (which show the domain points as small green dots).
The domain points are combined with the Bézier ordinates for
form Control Points (Pijk,
cijk )
A major application ( the major application in these pages) of the Bernstein--Bézier is the analysis of smoothness conditions between polynomials on neighboring triangles. The power of the Bernstein--Bézier form stems from the fact that algebraic (smoothness) conditions can be expressed, interpreted, and analyzed geometrically.
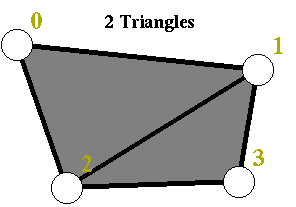
Suppose we are given two triangles, T with vertices V1, V2, and V 3, and U with vertices V0 , V1 , and V2 . Thus the triangles T and U share the edge e12 with vertices V 1 and V2, as indicated in the nearby figure.
We write the polynomial p on T in the form (3) and the polynomial q on U as
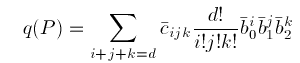 (4)
(4)
where the bar indicates barycentric coordinates and Bézier ordinates with respect to the triangle U.
We ask under what conditions do the polynomials p and q coincide along the edge e12 . Along that edge b3 is zero. Similarly, on U the barycentric coordinate multiplying V0 is zero.
Thus
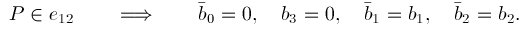 (6)
(6)
It follows that equating the two restrictions along e 12 gives the condition
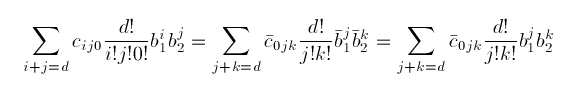 (7)
(7)
which is true if and only if
 (8)
(8)
We have thus obtained the geometric criterion:
The polynomials on the two triangles will join continuously if and only if the control points above the common edge coincide.
Since we always want at least continuity between neighboring polynomial pieces we do not distinguish the domain points along an edge shared by two neighboring triangles.
Differentiability conditions are more subtle. We ask for conditions under which first order derivatives of p and q join continuously across e12 . Thus we differentiate both p and q, restrict each to e12, and equate coefficients. However, the barycentric coordinates are not independent variables (since they add to 1) and so we cannot differentiate with respect to them.
Instead we consider directional derivatives. Let e denote a direction, i.e., a vector in the plane. (Often this is an edge of a triangle which accounts for the notation e .) We denote differentiation in the direction e with D. Thus
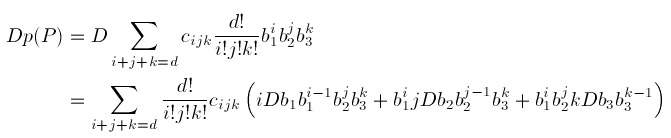 (9)
(9)
Reorganizing the sum gives the derivative in Bernstein-Bézier form:
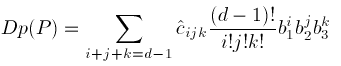 (10)
(10)
where
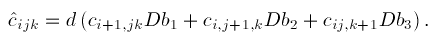 (11)
(11)
Note that since the barycentric coordinates are linear functions their derivatives are constants.
Doing the same on the triangle U and then equating coefficients gives rise to the algebraic conditions
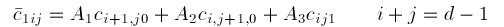 (12)
(12)
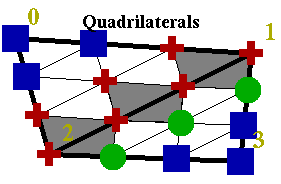
For each i and j, equation (12) relates four coefficients whose domain points form a quadrilateral in the domain and whose control points form a quadrilateral in space.
The quadrilaterals of domain points are illustrated in the nearby figure for the case d=3. The quadrilaterals themselves are gray, the domain points corresponding to the right hand side of (12) are red, those on the left hand side are green, and domain points not relevant to the smoothness conditions are blue.
The coefficients A1, A2 , and A3 can be derived algebraically. But much insight can be gained, and the power of the Bernstein-Bézier form can be appreciated, by the following geometric argument:
The coefficients in (12) are independent of the polynomial degree d. Consider them in particular for the case d=1 where the polynomials p and q are linear. Two linear functions join differentiably if and only if they are identical. Note that for general d
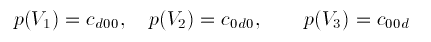 (13)
(13)
Thus the control points at the vertices of T lie on the graph of the function p. It follows that the piecewise linear function will be differentiable if and only if the control points at the vertices of T and U lie in the same plane!
If d>1 we still have the same algebraic relationships between the control points at the vertices of the gray quadrilaterals. However, the small quadrilaterals are similar to the quadrilateral formed by T and U. The geometric interpretation of the algebraic conditions is therefore the same: The control points at the vertices of the gray quadrilaterals must be in the same plane for each quadrilateral!. The planes may differ from quadrilateral to quadrilateral, but each quadrilateral of control points (in three dimesnional space must be planar. We have thus obtained the geometric criterion:
The polynomials on the two triangles will join differentiably if and only if for each quadrilateral there is a plane in 3-space that contains the four control points at the vertices of the quadrilateral.
It is now also clear that the Ai in (12) are the barycentric coordinates of V0 with respect to T, i.e.,
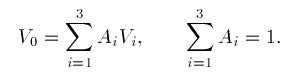 (14)
(14)
Higher order differentiability does not possess a geometric interpretation that is quite as striking as the first order differentiability conditions. Algebraically the r-th order conditions are given by
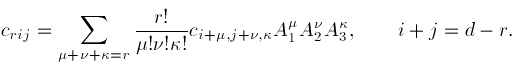 (15)
(15)
They also involve quadrilaterals, but they are larger than in the first order ( C 1 ) case and they overlap.
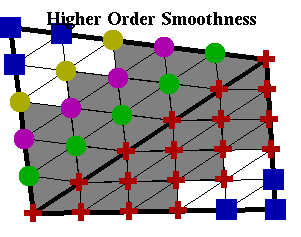
The nearby figure illustrates these conditions for the case where the polynomials d=5 and the degree of smoothness r=3.
The overlapping quadrilaterals are again drawn in gray. The coefficients entering the Right hand side of (14) are marked in red. Coefficients not entering any smoothness conditions are marked in blue. Coefficients determined by the first order conditions are green, those determined by the second order conditions are cyan, and those determined by the third order conditions, magenta.