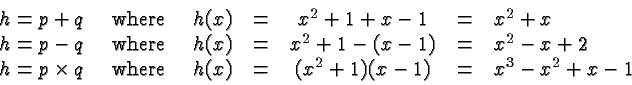A polynomial ![]() (in a variable
(in a variable ![]() ) is a function or an
expression that can be evaluated by combining the variable and
possibly some constants by a finite number of additions,
subtractions, and multiplications. Note that the list excludes
divisions (although a number like
) is a function or an
expression that can be evaluated by combining the variable and
possibly some constants by a finite number of additions,
subtractions, and multiplications. Note that the list excludes
divisions (although a number like
![]() would be considered
a constant). Also excluded are
radicals like
would be considered
a constant). Also excluded are
radicals like ![]() although a number like
although a number like ![]() would be (again) considered a constant.
When it matters we use the phrases polynomial expression or
polynomial function, but more frequently we use just the word
polynomial by itself.
would be (again) considered a constant.
When it matters we use the phrases polynomial expression or
polynomial function, but more frequently we use just the word
polynomial by itself.
A polynomial can always be written in standard form as
The
function ![]() is also a polynomial. It is called the
zero polynomial (or the zero function.) Its degree is
undefined,
is also a polynomial. It is called the
zero polynomial (or the zero function.) Its degree is
undefined, ![]() , or
, or ![]() , depending on the author. You
don't have to worry about the degree of the zero polynomial in this
class.
, depending on the author. You
don't have to worry about the degree of the zero polynomial in this
class.
Some examples will illustrate these concepts:
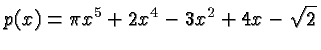 is a polynomial
of degree 5 with
is a polynomial
of degree 5 with
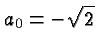 .
.
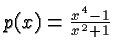 is a polynomial despite the apparent division because
is a polynomial despite the apparent division because
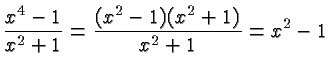
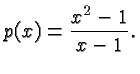
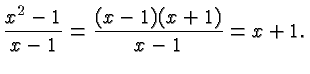
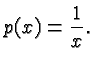
Don't get distracted by the subtlety of some of these examples. Usually it will be true that if you see a radical, an absolute value, or a division by an algebraic expression, then the expression or function in question is not a polynomial. But it is important to understand and appreciate the definition of the term polynomial with all its subtleties and ramifications.
Polynomials are important because they occur in applications and they
have nice properties: they are defined for all values of the variable,
and their graphs are smooth. Indeed, polynomials occur so frequently
that there is a whole language associated with them. The terms
involved are defined here, and you can also find their definitions in
virtually any ordinary dictionary of the English language. Throughout
let
The constant
You can add, subtract, and multiply polynomials and get a new
polynomial. On the other hand, the ratio of two polynomials is
usually not a polynomial. Rather than memorizing a number of rules
for the various operations you should recognize that they
are just the ordinary rules underlying all
algebra, such as the distributive law and the commutative and
associative laws of multiplication and addition.
A few examples illustrate the idea.
Let
Remember that you multiply
powers with the same base by adding the exponents. This implies
that the degree of the product of two polynomials is the sum of the
individual degrees. If you add (or subtract) two polynomials of
different degrees then the degree of the sum (or difference) is the
larger of the two individual degrees. If the two polynomials have the
same degrees then the degree of the sum or difference is that same
degree unless the leading coefficients cancel, in which case the
degree of the sum or difference is less. Don't attempt to memorize
these facts, instead make up some examples, think about the mechanism
of the operation, and then work out the details from your understanding
when you need them.
![]() be defined as in
be defined as in ![]() above, with
above, with ![]() .
.
![]() is the leading coefficient of
is the leading coefficient of ![]() , and
, and
![]() is its constant term. A polynomial with only one
non-zero coefficient (such as
is its constant term. A polynomial with only one
non-zero coefficient (such as ![]() ) is a monomial, one with
two such coefficients (like
) is a monomial, one with
two such coefficients (like
![]() ) is a binomial, and
one with three such terms (such as
) is a binomial, and
one with three such terms (such as
![]() but more likely
and frequently a polynomial of degree 2 like
but more likely
and frequently a polynomial of degree 2 like ![]() ) is a
trinomial. Polynomials of low degree occur so often that each degree
has been given a special name as listed in the following table:
) is a
trinomial. Polynomials of low degree occur so often that each degree
has been given a special name as listed in the following table:
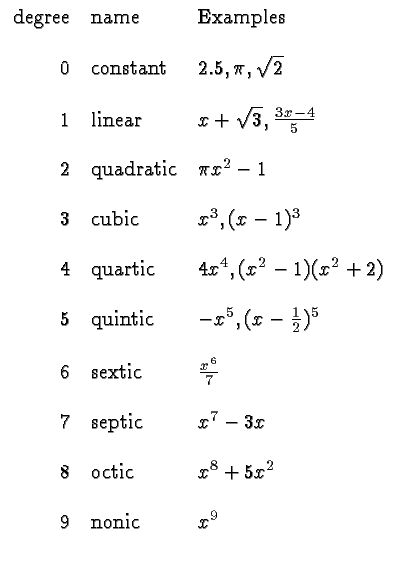
Combining Polynomials
![]()
![]() can be defined as follows:
can be defined as follows: