Numerical Analysis and Scientific Computing
Faculty involved
Peter Alfeld, Elena Cherkaev, Yekaterina Epshteyn, Aaron Fogelson, Fernando Guevara Vasquez, Christel Hohenegger, Akil Narayan, Braxton Osting, Jingyi Zhu.
Our group focuses on analysis and implementation of
- Finite Element Methods: Continuous Galerkin (CG) and Discontinuous Galerkin (DG)
- Finite Difference methods
- Central-Upwind Finite Volume Schemes
- Difference Potentials Method
- Efficient Algorithms for Inverse Problems and Optimization
- Multivariate approximation theory
- High-order numerical methods
With applications to:
- Computational fluid dynamics
- Flow in porous media
- Shallow water models
- Biomedical Applications
- Material sciences
- Inverse problems
- Electromagnetic and optic problems
- Optimal design of structures
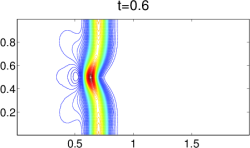
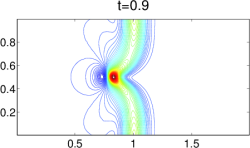
A numerical simulation of 2D Saint-Venant system of Shallow Water equations. (from “Well-Balanced Positivity Preserving Central-Upwind Scheme on Triangular Grids for the Saint-Venant System”, S. Bryson, Y. Epshteyn, A. Kurganov and G. Petrova)
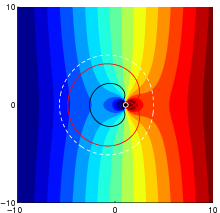
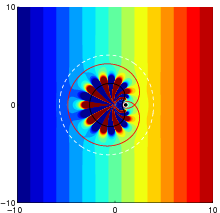
Cloaking with active sources for the Laplace equation in 2D. (from “Active exterior cloaking for the 2D Laplace and Helmholtz Equations”, F. Guevara Vasquez, G. W. Milton, D. Onofrei)

Let $\lambda_1(M,g)$ denote the first nontrivial Laplace-Beltrami eigenvalue of a closed Riemannian surface. The first conformal eigenvalue is defined by the eigenvalue optimization problem of maximizing $\lambda_1(M,g)$ as $g$ varies within a conformal class $[g_0]$ of fixed volume, $\text{vol}(M,g) = 1$. Plotted here is the conformal factor which attains the first conformal eigenvalue for a “Homer Simpson surface”. (from “Maximization of Laplace-Beltrami eigenvalues on closed Riemannian surfaces”, C.-Y. Kao, R. Lai, and B. Osting)
Webmaster: Fernando Guevara Vasquez. (Created by Yekaterina Epshteyn and FGV)