
Office: JWB 310
Office phone: (801)581-6495
Phone messages: (801)581-6851
Fax: (801)581-4148
NOTE new E-mail: graeme.milton?utah.edu (alias for u0028185?utah.edu) ,

Summary of Some Major Accomplishments
Publications since 2005, categorized by topic
List of publications by and about Graeme Milton with thanks to Nelson Beebe for producing it.
Notable recognitions include a 1988 Sloan Fellowship , an inaugural 1988 Packard Fellowship , the 2003 Ralph E. Kleinman Prize of the Society for Industrial and Applied Mathematics, the 2007 William Prager Medal of the Society for Engineering Science, the 2012 first competitive Rolf Landauer Medal of the International ETOPIM Association, and most recently the 2015 Levi-Civita Prize



Kshiteej Deshmukh and myself proposed a new type of time interface in the paper An energy conserving mechanism for temporal metasurfaces.
Fernando Fraternali, Narinder Singh, Ada Amendola, Gianmario Benzoni and myself conceptualized a new design for earthquake isolators in the paper A biomimetic sliding–stretching approach to seismic isolation that was highlighted in the Nature article The 3D print job that keeps quake damage at bay : see the video A novel seismic isolator with an anthropomorphic character .
My 2002 book "The Theory of Composites" is now back in print as a SIAM Classics book in Applied Mathematics
Also, now available in its entirety in a no-print version here is the book Extending the Theory of Composites to Other Areas of Science, with four chapters coauthored with Maxence Cassier , Ornella Mattei , Moti Milgrom , and Aaron Welters ,

kindly reviewed by Yury Grabovsky in SIAM Book Review and by Pradeep Sharma in Imechanica and in the Journal of Applied Mechanics To support low cost publication of research books, if you like the book please think about or ask your librarian to purchase a hardback copy. Only $80! Available here: Extending the Theory of Composites to Other Areas of Science
A snapshot of what is inside the book can be found in these slides

I have just made available the latex template file containing what I find to be useful macros, producing a sample pdf. Also now available for download are the bibtex files tcbook.bib and newref.bib with many references related to my research. tcbook.bib are those in my book "The theory of composite materials. Nelson Beebe is thanked for his help with these files."


see also the Nature News and Views Nature Article of Masaya Notomi.
The group of Martin Wegener produced the World's first Hall-coefficient reversal material, in the paper Experimental Evidence for Sign Reversal of the Hall Coefficient in Three-Dimensional Metamaterials based on a simplification of an interlocking ring design that in the papers Homogenization of the three-dimensional Hall effect and change of sign of the Hall-coefficient ( Hal.archives Version ) and Reversal of the Hall coefficient sign under homogenization , Marc Briane and I proved would reverse the Hall-effect back in 2007. This result (called by Wegener's group a "mind-boggling prediction") overturns the notion, found in many textbooks, that the Hall coefficient tells one the sign of the charge carrier. Inspiration for the geometry came from the chainmail artist Dylon Whyte and from joint work with Vincenzo Nesi. With D. Manceau we proved the reversal is impossible in two-dimensions. We also discovered the Parallel Hall Effect where the induced electric field is parallel to the magnetic field, and Wegener's group numerically and experimentally verified this too, with a simpler microstructure.

Our work on ideal climbing ropes (also available on ArXiv ) made it to the front cover of climbing magazine . Direct link here . A once in a lifetime achievement!
See also the news release of Lee Siegel

See the news release by Paul Gabrielsen describing our work on analytic materials, New math tools for new materials , and the accompanying paper also available on ArXiv. This paper also reviews other exact solutions in inhomogeneous media and the subject of metamaterials, providing a proper historical perspective.

See below some of the many articles related to our work on cloaking. It could be that our 2006 paper On the cloaking effects associated with anomalous localized resonance (submitted in October 2005, preceding the cloaking papers of Leonhardt and Pendry, Schurig, and Smith ) was the first to introduce the word "cloaking" into the scientific literature, outside computer science. With 12,815 downloads our paper Quasistatic cloaking of two-dimensional polarizable discrete systems by anomalous resonance was the most downloaded paper in 2007 amongst all 12 journals of the Optical Society of America.

See the articles below related to pentamode materials a new class of material that we devised in the 1995 paper Which Elasticity Tensors are Realizable? also available here In 2012, before they built pentamodes the group of Wegener in the paper, ''Tailored 3D Mechanical Metamaterials Made by Dip-in Direct-Laser-Writing Optical Lithography'' wrote: ''In addition, the ''holy grail'' of mechanical materials, namely pentamode materials, that can be seen as the mother of all materials, might become accessible as well. Pentamodes, suggested by Milton and Cherkaev in 1995, are solids that behave like fluids with a very small effective shear modulus.'' Pentamodes can be made anisotropic and in this way one gets a new sort of "anisotropic liquid", that instead of supporting a hydrostatic loading, supports a loading that is a combination of hydrostatic compression and shear, but is compliant to loadings in the orthogonal five-dimensional subspace of the 6-dimensional space of symmetric 3 by 3 matrices.


Below is a figure from our landmark paper Optical and dielectric properties of partially resonant composites (with the most relevant text being highlighted) that marked the discovery of anomalous resonance and ghost sources
(see also the introduction of a draft paper Unusual resonant phenomena where ghost image charges appear in the matrix doi:10.13140/RG.2.1.1477.5283).
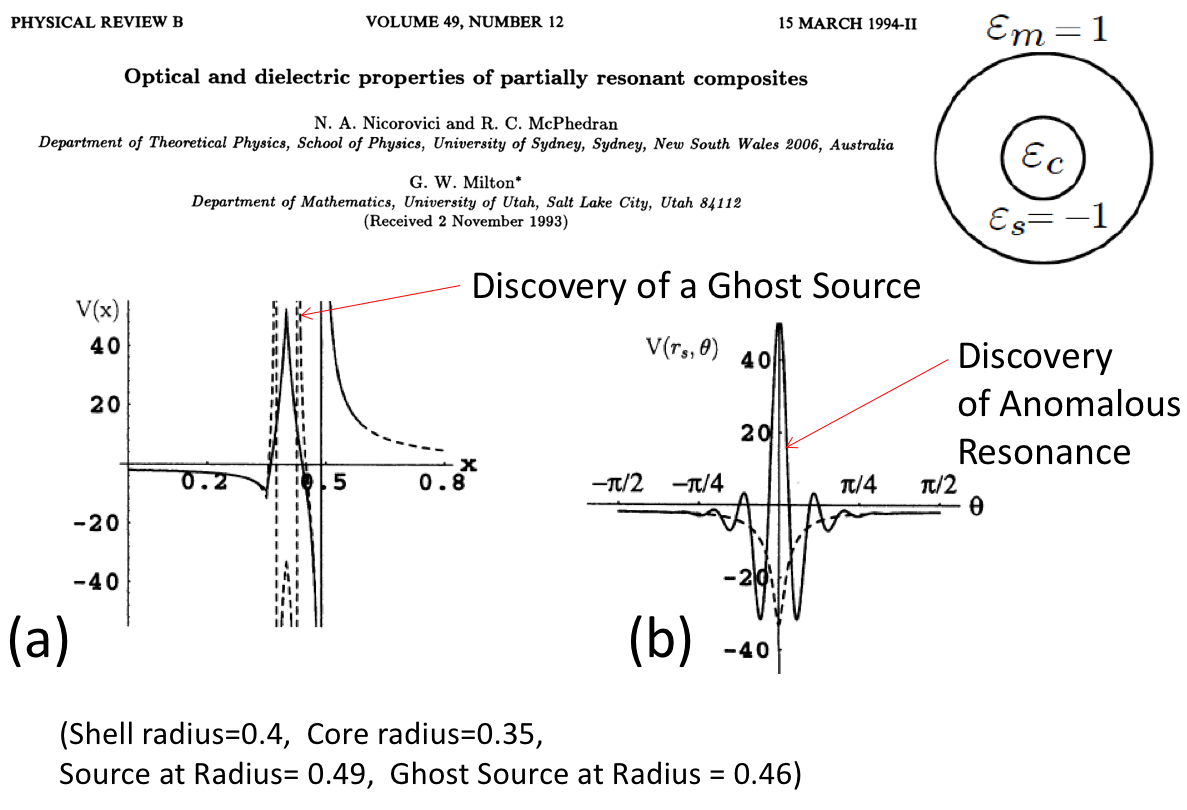
This later turned out to be the essential mechanism for explaining
the so-called
superlenses or perfect lenses,
for which Sir John Pendry received the
Kavli Prize.
.
In fact the structure we were analysing would now be called a quasistatic ("poor mans") magnifying superlens, and indeed we discovered it magnified the core.
Interestingly as shown in the paper
Interestingly as shown in the paper
Opaque perfect lenses
for a point dipole source turned on within a distance d/2 of a "perfect lens" of thickness d and emitting
constant power the long-time transmission is zero not one! All the power gets pumped into the anomalously
resonant fields. In fact the source does not radiate behind the lens either: this is an example of
cloaking due to anomalous resonance, first discovered in the paper
On the cloaking effects associated with anomalous localized resonance.
For some insight into the history of anomalous resonance see the SIAM news article
Anomalous Localized Resonance and Associated Cloaking
We were the first to discover ghost sources, not Sir John Pendry

Translation, thanks to my Russian friends, of Dolin's 1961 Paper, that marks the birth of Transformation Optics

Talk slides, including some talks given by my coauthors

Graeme Milton was born in Sydney, Australia, in the beautiful beach town of Manly . He received outstanding public education at the Wahroonga Bush School , Kur-ring-gai and Killarney Heights High Schools getting 7th place in the State High School Mathematics exam. Following this, he obtained an undergraduate and Master's degree in Physics at the University of Sydney where he had the distinction of receiving the University Medal with the lowest grade point average. His undergraduate honors' thesis, Theoretical studies of the transport properties of inhomogeneous media, under the direction of Ross McPhedran , introduced him to the field of composite materials, resulting in the publication Bounds on the complex dielectric constant of a composite material that received more reprint requests than any of his subsequent papers (in the days when people mailed reprint request cards). He did his Ph.D thesis Some Exotic Models in Statistical Physics at Cornell University Physics Department with Michael E. Fisher . Following this he did a postdoc with Michael Cross at Caltech as a Weingart Fellow. George Papanicolaou suggested he apply for an assistant professorship at the Courant Institute, where he got tenure and was promoted to Associate Professor after two years to Associate Professor, and later to Full Professor. However, the attraction of the outdoors (downhill and cross-country skiing, hiking, mountain biking, and road biking) in spectacular Utah pulled him, with the help of Ken Golden , Paul Fife , and Benny Rushing , to the University of Utah Mathematics Department, where in 1999 he became Distinguished Professor, and served as department chair from 2002-2005 . He is especially grateful for the mentoring he received during his career.