The Natural Cosine and Sine Curves
The natural cosine and sine curves describe the horizontal and vertical coordinates of a point on the unit circle in terms of the counterclockwise distance along the circle to the point from a reference point where the circle intersects the positive horizontal axis.
The Natural Sine Curve
In the first animation, a point marked
by a red dot travels at unit speed counterclockwise about the circle. Its vertical
coordinate, ![]() , is tracked
by a horizontal red line.
, is tracked
by a horizontal red line.
The circular distance from the reference point to the red dot, ![]() ,
is measured by a circle of the same radius rolling without slipping along the
horizontal axis with the same speed as the red dot. Observe how the rolling
circle completes each quarter turn in the same time as the red dot.
,
is measured by a circle of the same radius rolling without slipping along the
horizontal axis with the same speed as the red dot. Observe how the rolling
circle completes each quarter turn in the same time as the red dot.
Finally, the intersection of a shorter vertical red line through the center of the rolling circle with the horizontal line through the red dot describes the natural sine curve in purely geometric terms. An interactive implementation described below can be used to observe other relationships geometrically.
The Natural Cosine Curve
In the second animation, the horizontal
coordinate of the revolving point, ![]() ,
is tracked by a vertical red line. To view the horizontal coordinate as a
dependent variable in the usual way, we must turn our heads clockwise by a quarter
circle, the only reason we have treated "y" ahead of "x".
,
is tracked by a vertical red line. To view the horizontal coordinate as a
dependent variable in the usual way, we must turn our heads clockwise by a quarter
circle, the only reason we have treated "y" ahead of "x".
For this reason, we wish to measure the distance the red dot has travelled from the reference point as an independent variable in the usual way, along an axis a quarter circle clockwise from the dependent variable, which in this case is the negative vertical axis.This is again measured by a rolling circle which starts from zero when the red dot is on the reference point.
The interesection of another short red line through the center of this rolling circle with the red line through the red dot describes the natural cosine curve in purely geometric terms. An interactive implementation demonstrates other relationships involving the natural cosine curve.
The derivatives of the natural cosine and sine
Another configuration of the interactive animations can be used to understand the relationships involving rates of change of the natural sine and cosine: why the derivative of the natural sine is the natural cosine and the derivative of the natural cosine is minus the natural sine (which is not exactly true for the corresponding functions in terms of degrees!) click the buttons to show the position vector, the velocity vector, and the velocity vector based at the origin for the rotating point. The fact that the velocity vector equals the position vector rotated a quarter circle counterclockwise may be written
![]()
More details on this relationship and the connection to the the slope of the tangent line to the graphs are given below. The basic animation of the cosine and sine curves together may be found here, and an interactive implementation of the cosine and sine animations simultaneously is here.
Controlling the interactive animations
The control panel allows you to pause and reset the animation as well as to play continuously or in step-by-step mode, forward or backward.(The function of each button is revealed by placing the cursor over the button.)
The elements of the animation may be individually hidden or displayed by toggling the buttons with the corresponding icons, i.e., the rotating red dot, rolling circles, crosshairs, the circle and graphs themselves. Yellow dots mark the projections of the rotating point on the horizontal and vertical axes, which oscillate in what is known as "simple harmonic motion".
Features not visible in the default configuration may also be viewed, including the position, velocity, and acceleration of the rotating point. The latter two are displayed both at the head of the position and velocity vectors, respectively, and translated to the origin. Other unit vectors symbolize the unit speed of the rolling circles.Two more buttons display the tangent lines of both graphs. It is interesting to view the tangent lines with the graph itself hidden and ponder reconstructing the sine and cosine curves from their tangents.
Some especially useful points on the circle and graphs corresponding to every eighth and twelfth of the way around the circle are marked and labelled. When the animation is paused at these points, the remaining buttons may be used to view the corresponding right triangles inside the unit circle, as well as the corresponding horizontal and vertical components of the tangent lines
A favorite configuration displays just the horizontal and vertical projections of uniform circular motion, each undergoing simple harmonic motion. Notice that the two yellow dots are opposite each other on an invisible circle of half the radius rolling inside the larger circle. Dale Meier has created a beautiful extension and exploration of this configuration. Observe the harmonic motions swept out by points on a circle rotating around the inside of a circle of twice. Make sure to click the "Multi" box!
There are 48 frames per revolution, so that each step corresponds to 1/48 of a circle, or 7.5 degrees. Four clicks of the step forward button advances the rotating point by 1/12 of a circle, or 30 degrees, and six clicks advances by 1/8 of a circle, or 45 degrees.
In some browsers, it is possible to zoom into and out of the animation.
More mathematical relationships visualized
The red dot has been revolving around the unit circle forever and will continue on forever as indicated by the extensions of the cosine and sine curves to the left and right. The motions of the horizontal and vertical coordinates repeat but each revolution forward or backward adds or subtracts
to/from the distance from the reference point. Symbolically:
![]()
and
![]()
This illustrates the advantage of using the symbol ![]() (see below) which represents one full revolution
or circumference of a circle. Unfortunately, the symbol
(see below) which represents one full revolution
or circumference of a circle. Unfortunately, the symbol ![]() represents
half a circle, so that instead of referring to three quarters
represents
half a circle, so that instead of referring to three quarters
of a circle
![]()
we refer to three halves of half a circle
![]()
(usually spoken "three pi over two") which is about as natural as calling three quarters of an hour "three half hours over two"!
Turning our heads a quarter circle counterclockwise, the positive vertical axis takes the role of the positive horizontal axis. If we wait until the red dot reaches the top of the circle (the right side from this perspective) the originally vertical motion, now looks identical to the original horizontal motion, only shifted by that quarter of a circle in time or circular arc length. This is represented symbolically:
![]()
In terms of the graphs, when we turn our heads a quarter circle clockwise, we make the dual observation that the graph of the natural cosine is the same as the graph of the natural sine shifted (left) by one quarter period:
![]()
Viewing these two circular functions and their rates of change simultaneously
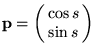
can greatly simplify and enhance our understanding, and provide a natural starting point (or definition!) from which other relationships and perspectives such as addition formulas, series, trigonometry, etc., can be easily understood.
Let us hide the graphs for a moment and view just the revolving point along with its the position and velocity vectors. The velocity must be perpendicular to the position, since any component of change in the direction of the position would change the point's distance from the origin, which is assumed constant, and equal to one. Since the points speed is also one, the velocity vector must be the unit vector a quarter circle counterclockwise (the direction of the rotation) from the position vector. Now view the velocity vector based at the origin. Mathematically, this is considered equivalent to the one based at the position vector, in just the same way as the fraction 3/6 is considered equivalent to 1/2. It is easy to see using similar triangles that the components of the velocity vector are
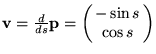
This gives the rate of change relationships a simple and natural meaning.
These relationships may also be viewed in terms of the slope of the tangent lines of the cosine and sine graphs. Pause the animation at any of the "keypoints", for instance by clicking reset and stepping forward four clicks (one twelfth of a revolution around the circle). Now view the sine graph, its tangent line, and tangent components. Observe that the vertical component of the tangent line is give by the vertical component of the velocity of the red dot (view the velocity vector at the red dot!) horizontal component is always 1, since the independent variable is just the arc length s which the point has travelled around the circle. The slope of the tangent line is therefore equal to the vertical component of the velocity vector, and again we have
![]()
just interpreted differently. Doing the same for the cosine graph visualizes
![]()
in terms of the slope of the tangent line.
If we repeat the same steps we used to derive the velocity vector from the position vector, now going from the velocity vector to its rate of change, the acceleration vector, and then the acceleration vector at the origin, the relationships are perfectly analogous. The acceleration is the velocity rotated a quarter circle counterclockwise, so again by similar triangles, we interchange the coordinates and negate the first one:
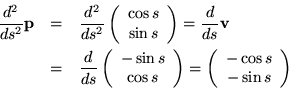
The arc-length parametrization of the unit circle by the cosine and sine functions
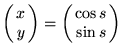
is easily and naturally defined by the essential and intuitive property that the rate of change of positon is given by rotating the position a quarter circle counterclockwise:
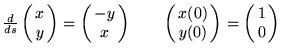
Starting from these relationships, it is quite easy to derive the addition formulas, Pythagorean relation, series representations for the cosine and sine. We believe that the power and beauty of calculus is best demonstrated by this simple approach. (Consider the alternative of defining the adjacent over hypotenuse and opposite over hypotenuse of a right triangle as real valued functions and proving the differentiation rules from these definitions just as rigorously. Similarly, why contrive a proof of the derivative rule for the natural exponential, when it is really the definition?)
Precalculus treatments of the addition formulas, connection with complex numbers, the Pythagorean relation, and the geometric interpretation of the dot product may also be be motivated, unified and understood from the rotational point of view.
The symbol ![]() used in the graph labels, which conceptually simplifies the notation and discussion
for many aspects of circular functions was introduced in the article "Pi
is wrong!" which appeared in the Mathematical Intelligencer, Summer
2001. It is typeset with a one line macro
created by Richard Palais.
used in the graph labels, which conceptually simplifies the notation and discussion
for many aspects of circular functions was introduced in the article "Pi
is wrong!" which appeared in the Mathematical Intelligencer, Summer
2001. It is typeset with a one line macro
created by Richard Palais.
The author wishes to thank the late Prof. Benny Rushing for inspiration and support, and multimedia artist Dale Meier who produced the beautiful and simple first implementation of this animation in real time as it was described to him, and has guided the later developments with his expert instruction in Flash and ActionScript.
The contributions, feedback, and encouragement of many others, including editors Tom Roby, Chandler Davis, and Tom Farmer, colleagues Nick Korevaar, Blake Thornton, Andrej and Elena Cherkaev, Morris Hirsch of U.C. Berkeley, and my family, have been especially appreciated.