RANDOM WALKS AND SIMULATION
Summer 2002 REU: About Random Walks, Simulation, and Related Links

Department of Mathematics, The University of Utah

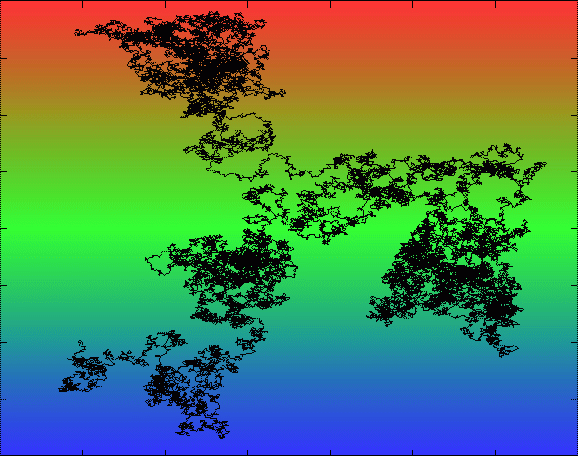Q. "What is a random walk?" you might ask. Here is a reasonably good description kindly provided by the Merriam-Webster Collegiate Dictionary on line:

"a process (as Brownian motion or genetic drift) consisting of a sequence of steps (as movements or changes in gene frequency) each of whose characteristics (as magnitude and direction) is determined by chance."

Perhaps the best place to start learning about random walks is by reading two very nice expository articles by G. Slade who is Professor of Mathematics at the University of British Columbia in Vancouver, Canada:

• Random walks (1996). American Scientist, 84, 146-153.
• Self-avoiding walks (1994). The Mathematical Intelligencer, 16, 29-35.

Q. "What is a simulation?" you might ask next. Here is a reasonably good description kindly provided by the Merriam-Webster Collegiate Dictionary on line:

"the imitative representation of the functioning of one system or process by means of the functioning of another."

Q. "What do random walks look like?" This is best answered by a simulation of the random walk. Here are two links to simulations of random walks:

• Jim Carlson, who is Professor of Mathematics at the University of Utah, has created this Java applet for simulations of 2-dimensional random walks. This page also contains interesting historical references to the connection to the Brownian motion, which is a random process popularized by the 1905 work of Albert Einstein.
• To see how 1-dimensional random walks evolve in time, also have a look at these Java simulations of Jim Carlson.

Related Links

We ran a search on Google, and found "over 164,000 links!" In other words, random walks really are an important fact of life to many mathematicians and non-mathematicians alike. The following is a minute sample of some interesting web pages related to random walks. None of these URL's require a deeper understanding of random processes than what is covered in a standard undergraduate course in probability. Here you can also find a number of interesting simulations of 2-D random walks.

• Center for Nonlinear Dynamics at the University of Texas sometimes maintains a number of pages of potential interest to our REU program. In particular, here you can find a rough-and-friendly description of random walks and related random processes; you can also find a few simulations here.
• Ray Bradley's links to various articles and simulations inspired by problems in computer science; the general theme here is the "self-avoiding random walk."
• Virtual Laboratories at the University of Alabama contains a probability primer that includes a description of random walks and related objects.
• The Computer-Integrated Construction Group at the National Institute of Standard and Technology contains , among other things, a number of "random walk visualizations" in materials science. Superb graphics!
• Department of Mathematics at Furman University maintains a nice (but a little slow) Java applet that simulates a two-dimensional random walk.
• The Harvey Project's simulation of 2-D random walk. [The reference to "diffusions" is non-standard.]
• The Robotics Institute at the Carnegie Mellon University has made this Pdf file that introduces a random walk model (or, more appropriately, a Markov chain model) in learning theory in computer science.
• The Computational Physics Group at the Oregon State University has published this page that includes a 2-D random walk simulation.
• Wolfram Research's "Mathworld;" it includes a rough description of random walks and their relation to other interesting random processes. Here you can find further links to some of the topics related to this REU.
• Alexei Sharov at the Department of Entomology at Virginia Tech maintains this URL, which contains a nice description of a standard application of random walks to population biology.

  REU 2002 Main Page

  Information and Forms for Applicants

  The Summer 2002 Research Program

  Reading List

  Disclaimer
  © 2002 by the Dept of Math. University of Utah