
The picture illustrates concepts of structural optimization.
- The problem of design asks for a layout of several materials within the designed body in order to maximize an integral characteristics.
- As a rule, an optimal design is made from optimal composites: fine scale alternating subdomains of different materials. In order to make optimal constructions one needs to understand properties of composites with extremal properties.
What kind of composites must be used an optimal construction?
The answer depends on the feature one wants to optimize.
Elasticity: some structural optimization problems, requirements to structures, and the math. formulations Maximal stiffness Maximal mean stiffness Maximal "responce" The minimization of the total energy stored in a construction (or the maximization of its integral rigidity under some fixed loading) requires the search for composites which store minimal energy under some given loading.
The problem is reduced to a non-stable variational problem of the minimization of the energy upon the structures.
Optimal structures: Specially oriented second-rank matrix laminates or "coated ellipses" in 2D, or third-rank laminates or "coated ellipsoids" in 3D.
The orientation of the optimal structures follows the axes of the stress tensor.
The minimization of the total energy stored in a construction under some uncertain or varying loading requires the search for composites which store minimal sum of energies under several loadings.
The problem is reduced to the minimization of the maximal eigenvalue of some operator upon the fields and the structures.
Optimal structures: third-rank matrix laminates in 2D, or six-rank laminates in 3D. The orientation of the optimal structures may follow the axes of the stress tensor of stay constant everywhere.
The minimization of other integral functionals, like the norm of the displacement etc. requires the search for composites which are simultaneously weak with respect to a loading and strong with respect to an orthogonal loading.
The problem is reduced to minimization of the sum of the energy under a loading and the complementary energy under some other loading.
The whole variety is not described yet. The variety of optimal structures include the matrix laminates, herring-bones, and something else...
Mathematics
Optimal design problems can be viewed as a special type of variational problems. Typically, they require minimization of an unstable (not weakly lower semicontinuous) functional. Therefore special relaxation methods are developed to find and effectively describe highly oscillating solutions of these problems. These methods includeSufficient conditions methods, particularly the Translation method. Searching for minimization sequences, particularly for laminates of a high rank. Necessary conditions and the stable extensions. Stability of optimal designs.
Optimal structures are generally unstable. Indeed, they concentrate the resistance capacities in certain directions to stay against a given loading, therefore they are extremely sensitive to the variation of the loadings. We are working on designs that compromise effectiveness and stability.
A simplest example of structural optimization
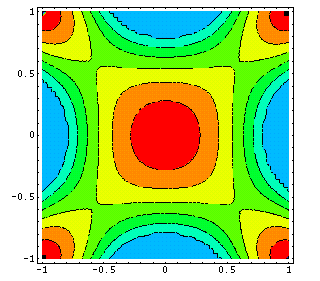
The next picture shows the crossection of the torsioned bar with maximal rigidity. The bar is assembled from two materials with different elastic moduli, the proportion of the materials in the design is fixed.
It has been proved (Lurie and Cherkaev, 1980) that an optimal project is made from either pure given materials or from laminates.
Here, the blue and the red domains denote the originally given strong and weak materials, the color reflects the volume fractions in optimal laminates, lines show their directions. The more is the norm of stresses, the more rigid is the optimal composite.
The International Society of Structural and Multidisciplinary Optimization
(ISSMO)
Back to the research page