Optimal Composites

Optimal composites show with extremal effective properties. Our main interest is to find structures of these composites and to find bounds of the range of their properties. The extremal composites are used in structural optimization, the bounds provide a priori information of the possible range of achievable properties.

The set of effective properties of all possible composites made from given materials is called G-closure of the set of original properties. The problem is to desribe the G-closure (or its components) for different sets of original materials.

The following picture shows the G-closure for two conducting materials and the best structures that correspond to boundaries of the G-closure.

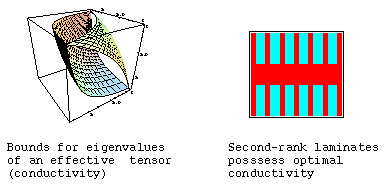
Mathematically, the problem of bounds and of extremal structures can be formulated as a nonconvex variational problem of minimization of the sum of energies/complimentary energies that a structure stores under different loadings. We have now a pretty detailed picture of structures of two-phase conducting and elastic materials, but the best structures of multiphase composites are mainly unknown. I am working on this extremely interesting and knotty problem. The difference between two-phase and multi-phase optimal structures is huge. It is similar to the difference between the black and white and the color TV.

The following picture shows the variety of the topology of optimal isotropic conducting two-dimensional three materials structure. Note the optimal topology of two-material mixtures us pretty clear: "good" material outside, "bad" material inside inclusions.

Large volume fraction of the best material, the swiss cheese topology (Milton, 1986) Small volume fraction of the best material; this material localizes inside the inclusion to compensate the properties of the worst material (Cherkaev, 1998)

Red color corresponds to the best conductor, yellow color - to the intermediate conductor, blue color - to the worst conductor. The contact directory in the Mathematics for Materials Web server is here: composites

Back to the research page


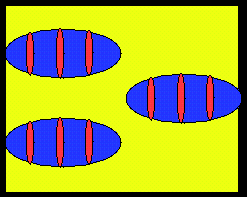Large volume fraction of the best material, the swiss cheese topology (Milton, 1986)	Small volume fraction of the best material; this material localizes inside the inclusion to compensate the properties of the worst material (Cherkaev, 1998)