Effective medium theory

Effective medium theory calculates effective properties for media with located symmetric inclusions. The approach leads to exact formulas for the effective conductivity. It was originated and discussed in [#!Bruggemann:1935:BVP!#,#!Bruggemann:1937:BVP!#,#!Hashin:1962:VATa!#,#!Christensen:19_79:MCM!#] and others. Specifically we discuss the structure of the ``coated spheres'' suggested in [#!Hashin:1962:VATa!#].

It should be mentioned that the structures obtained by using this method can also be obtained by using the described differential scheme. However, we feel that the description of the effective medium theory is helpful from both historic and aesthetic viewpoints.

Consider a homogeneous material with isotropic conductivity $\sigma_*$. Suppose we replace the medium in a disk of unit radius with the following two-phase configuration. The inner disk of radius $r_0 <1$ is filled with material $\sigma_1$, and the annulus $r_0< r< 1$ is filled with material $\sigma_2$. This configuration (see ) is called the coated circles (or, in three dimensions, the coated spheres).

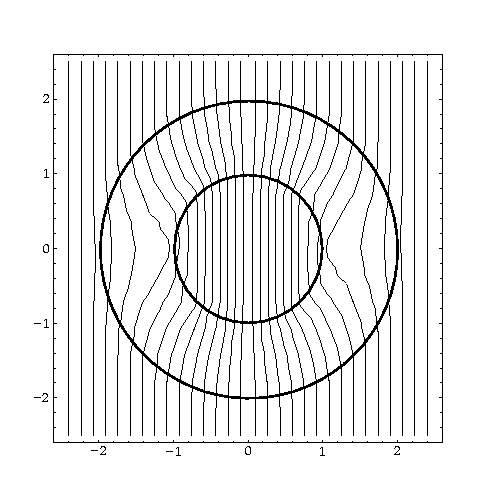
The geometry of coated circles\index{coated circles}. The field outside the external disk is homogeneous. The inner disk has higher conductivity than the effective medium, and the exterior annulus has lower conductivity than the effective medium. Observe the complete mutual compensation of the inclusion. The inclusion is ``invisible'' for an observer in a uniform external field.

Assume that the configuration is submerged into a uniform external field ${\bf e}(r,\theta) \rightarrow \cos \theta$, when $r \rightarrow \infty$. The corresponding potential $w$ tends to the affine function $w \rightarrow r \cos \theta$.

Suppose we manage to define the conductivity $\sigma_*$ so that the field everywhere outside of the inclusion is a constant vector: ${\bf e} = {\bf i}_1$. In polar coordinates, this condition takes the form

$${\bf e}(r,\theta) = [\cos \theta, \sin \theta] \quad \forall r>1.$$ (14)

In this case, we cannot detect the presence of the inclusion by observing the fields anywhere outside of the inclusion. Hence, we cannot distinguish the homogeneous configuration with conductivity $\sigma_*$ from a configuration with one, or several, or even infinitely many circular inclusions of the described type; see . In this case we call $\sigma_*$ the effective conductivity of a composite made of coated circles.

To find $\sigma_*$, we explicitly calculate the field everywhere in the configuration. The field satisfies the boundary value problem:

$$\left(\frac{\partial }{\partial r} r \left( \sigma_{rr} (r) \frac... ...theta} (r) \frac{\partial }{\partial \theta}\right)\right) w=0 \mbox{ in } R^2,$$ (15)

$$\lim_{r\rightarrow \infty} \frac {\partial w(r,\theta)}{\partial r} =\cos \theta,$$

and satisfies the jump conditions on the circles and the effective medium condition 14.

This boundary value problem allows for separation of variables; the solution $w$ has the form $w = R(r) \cos \theta$. The function $R(r)$ must satisfy the ordinary differential equation for $R(r)$

$$r {d \over d \, r} \left( r {d \over d \, r} \, R \right)- \frac{\sigma_{\theta \theta}}{\sigma_{rr}} R(r) =0$$ (16)

the conditions

$$\begin{array}{rlrl} R(0) & =0, & \quad R'(0) & =0, \\ \left... ... \\ \quad \lim_{r\rightarrow \infty} R & =r, & ~ & \end{array}$$ (17)

where $[x ]$ means the jump of $x$, and the condition 14. The conductivity $\sigma(r)$ is

$$\sigma(r)= \left\{ \begin{array}{llrl} \sigma_1 & \mbox{if} ... ...sigma_* & \mbox{if} & r & \in [ 1, \infty). \end{array}\right.$$

We assume that the potential is zero at $r=0$ (we can always assume this, because the potential is defined up to a constant), and we require the continuity of the field at $r=0$. The last condition in 17 says that the field in the system with the inclusion tends to a homogeneous field when $r \rightarrow \infty$. The remaining conditions express the continuity of the potential and of the normal current on the circles $r=r_0$ and $r=1$.

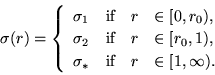
The solution to 16 that satisfies the conditions 17 has the form

$$w= \left\{\begin{array}{llrl} A_0 r \quad & \mbox{if} & 0 &... ... {B_2 \over r} & \mbox{if} & 1 &< r. ~ \\ \end{array} \right.$$ (18)

To define the four constants $A_0,~ A_1, ~ B_1$, and $B_2$ we use conditions 17.

The key point of the scheme is the following: We assign the constant $\sigma_*$ in such a way that $B_2=0$ or that the field is homogeneous if $r>1$. This way, 14 is satisfied.

Accounting for the constants, we have

$$\matrix{A_0= {{2\,\sigma_2}\over m_2\,\sigma_1 + (1 + m_1)\,... ...igma_2 \right)}\over {m_2\,\sigma_1 + (1 + m_1)\,\sigma_2}},}$$ (19)

and

$$\sigma_*=\sigma_{HS}= \sigma_1 {{(1 + m_1)\,\sigma_1 + m_2\,\sigma_2}\over {m_2\,\sigma_1 + (1 + m_1)\,\sigma_2}}.$$ (20)

Formula 20 shows the effective conductivity of the configuration. The conductivity was calculated in [#!Hashin:1962:VATa!#], where it was also proven that $\sigma_{HS}$ is the extreme isotropic conductivity that one can achieve by arbitrary mixing of two isotropic materials in the prescribed proportion.

Several generalization of the procedure were suggested.

A generalization of the procedure was suggested in [#!Milton:1980:BCD!#], which considered the geometry of ``coated ellipses'' (one inscribed into another) and found the explicit description of their effective properties. This time, the effective medium is anisotropic. The idea of the calculation is the same: We consider one ``coated elliptical inclusion,'' i.e., two ellipses in an unbounded domain and a homogeneous field applied at infinity. This time we use elliptical coordinates to separate the variables.

Another generalization is based on the construction by Shulgasser [#!Schulgasser:!#] who considered an invisible spherical inclusion from an anisotropic material with radial symmetry. In the workshop, we use a more sophisticated geometry placing an anisotropic material with radial symmetry into the outer layer of the coater spheres structure.

If the outer material is a laminate from radially oriented infinitesilmal thin layers and the nucleous is made out of one of the laminate's consistencies, then such geometry (the hedgehogs) models diffusive medium with inclusion.

If the layers in outer laminate are inclined to the radium, we obtain a spiral structure.

This construction is used in the Workshop.