Differential scheme

Developing the idea of laminates of a high rank, we come to a special class of laminates of infinite rank. Consider the following differential scheme: An infinitesimal portion of a pure material is added to the composite at each infinitesimal step. Such materials are described in many works, starting from [#!Bruggemann:1935:BVP!#]. They were rediscovered and systematically used in [#!Norris:1985:DSE!#,#!Lurie:1985:OPM!#,#!Avellaneda:1987:IHD!#], among other papers.

Consider the process of formation of a laminate composite. Suppose that a portion $d {\mu} \ll 1$ of material $D$ is added to the composite with the effective tensor $\Delta ({\mu})$ and that the periodic cell has volume ${\mu}$. The material is added in a infinitesimal thin periodic layers with the normal $n({\mu})$. The resulting composite cell has the volume ${\mu}+d {\mu}$ and an effective properties tensor denoted by $\Delta({\mu}+d {\mu})$.

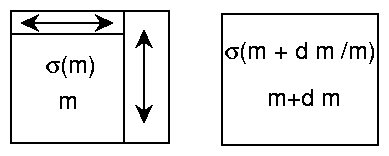Differential scheme

Let us compute $\Delta({\mu}+d {\mu})$ by using 8, where we set

$$m_1= {d {\mu} \over {\mu}}, \quad m_2 = 1-{d {\mu} \over {\mu}},$$

$$D_1=D, \quad D_2 =\Delta({\mu}), \quad D_{\mbox{\footnotesize {lam}}}=\Delta({\mu}+d {\mu}).$$

The relation 8 becomes

$$\Delta({\mu}+d{\mu})- \Delta({\mu}) = {d {\mu} \over {\mu}}\Psi(\Delta({\mu}), D, n) + o(d {\mu})$$

where

$$\Psi(\Delta({\mu}), D, n) = -[(\Delta ({\mu})-D) - (\Delta({\mu})-D) N (\Delta({\mu})-D)],$$

$$N= q[q^{T} D q]^{-1} q^{T}.$$

The function $\Psi$ depends on $n$ through $N=N(q)$, because $q$ is determined by $n: ~ q=q(n)$.

As $d {\mu}$ tends to zero, we obtain the differential equation

$${\mu} \frac{d}{d {\mu}}\Delta({\mu})= \Psi(\Delta, D, n).$$ (13)

This equation shows the rate of change of effective properties. It is integrated with respect to ${\mu} \in [0, 1]$. The functions $D=D({\mu})$ and $n= n({\mu})$ determine the structure of the composite. We assume that different materials with properties $D({\mu})$ are added to the composite in different ``times'' ${\mu}$. We also assume that $n= n({\mu})$: The direction of laminates is generally changed during formation of the composite.

This scheme is effectively used in our Workshop to the Workshop to compute effective properties of the Hedgehogs, Pipe-brushes, end similar structures. It is flexible and robust.