Laminates of a rank

We now describe more complicated structures called ``laminates of high rank''. They are defined by an iterative process.

Laminates of second rank

Let us consider a laminate structure as an anisotropic material with the effective properties tensor $L(D_1, D_2, {\mu}, n)$ that depends on the initial material's properties $D_1, D_2$ and on structural parameters: the normal $n$ and the volume fraction ${\mu}$ of the first material.

Choosing two different sets

$$\left\{ n^{(11)}, {\mu}^{(11)}\right\} \quad \mbox{ and} \quad \left\{ n^{(12)}, {\mu}^{(12)}\right\}$$

of values of the last two parameters, we may define two different laminates with the effective properties tensors

$$D^{(11)}=L(D_1, D_2, {\mu}^{(11)}, n^{(11)}) ~\mbox{ and } ~ D^{(12)}=L (D_1, D_2, {\mu}^{(12)}, n^{(12)}).$$ (10)

Structure of a second rank laminate

The laminate of second rank is the laminate structure with normal $n^ {(2)}$ and fraction ${\mu}^{(2)}$ made of materials $D^{(11)}$ and $D^{(12)}$ (see 9):

$$D_{l}^{(2)}=L (D^{(11)}, D^{(12)}, {\mu}^{(2)}, n^{(2)}).$$ (11)

This structure depends on the following structural parameters: normals $n^ {(11)}, n^{(12)}, n^{(2)}$ and concentrations ${\mu}^{(11)}, {\mu}^{(12)}, {\mu}^{(2)}$. It contains the materials $D_1$ and $D_2$ in the volume fractions

$$m_1={\mu}^{(11)} \, {\mu}^{(2)} + {\mu}^{(12)} \left(1-{\mu}^{(2)} \right), \quad m_2=1 - m_1,$$

respectively.

Laminate of an arbitrary rank By repeating this procedure one can obtain laminates of any rank. The procedure assumes separation of scales: The width of laminates of each succeeding rank is much greater than the width of the previous rank. The obtained composite is considered as a homogeneous effective material at each step.

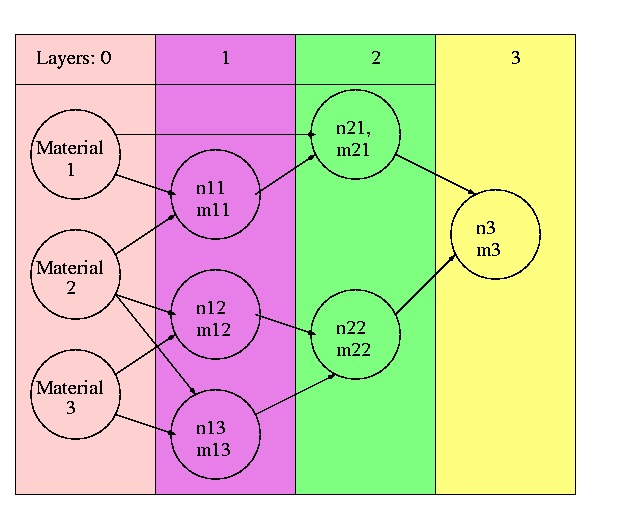
The tree correspond to a scheme of constructing of a laminate of fourth rank

At the same time, all widths are much smaller than the characteristic length of the domain and of the scale of variation of exterior forces. Under these assumptions, it is possible to explicitly calculate the effective properties of the high-rank laminates. Namely, the laminates of the $k$th rank correspond to the tensors $D^{(k)}$ determined by the normal $n^{(k)}$ and the concentration ${\mu}^{(k-1)}$:

$$D^{(k)}_l=L(D^{(k-1,1)}, D^{(k-1,2)},{\mu}^{(k-1)}, n^{(k)}),$$ (12)

where $D^{(k-1,1)}$ and $D^{(k-1,2)}$ are two tensors of the $(k-1)$th rank. The hierarchical structures were first considered in [#!Bruggeman:1930:EK!#], where also their effective characteristics where introduced. They were first used in [#!Schulgasser:1976:RBS!#,#!Schulgasser:1977:BCS!#] to describe polycrystals and in [#!Milton:1981:BCP!#,#!Lurie:1982:ROD!#] to optimize properties of composites.

In dealing with more than two mixing materials, one can add them one by one to the laminate.

Our workshop allows for modeling of these structures

Fields in inner substructures To calculate the fields in a laminate of a high rank one must first compute the effective properties of the substructures that form the composite and find the matrices $K_i$. Then one computes the fields using 6. The procedure starts from the outer layer (of the rank $k$), and the field $v_1^k$ and $v_2^k$ in two largest layers are linked with the external field $v_0$:

$$v_1^k= K(k, 1) v_0 \quad v_2^k= K(k, 2) v_0;$$

Then one iteratively computes the fields down the tree of layers by simply multiplication of the transform matrices. For example, the field a three-level-deep branch $K_3$ is computed as:

$$K_3=K(k, 1) K(k-1, 1, 1)( K(k-2, 1, 1, 2)$$

where the coefficient $K(k-1, 1, 1)$ transforms the field from the layer one in the last partition to the layer 1 in the subpartition of this layer, end so on.

to the Workshop

The special classes of laminates are describe below, in the next section 5