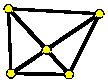


A singular vertex in a triangulation is an interior
vertex of degree 4 whose edges form two parallel pairs. Put
less technically, it is the intersection of the diagonals in
a convex quadrilateral, as shown in the small figure in the
title.
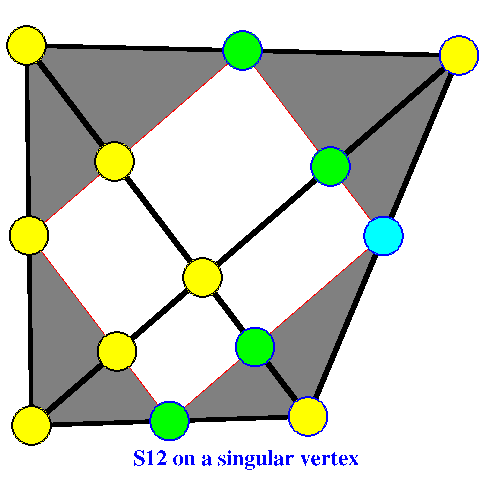
The Figure "S12 on a singular vertex" shows a
singular vertex and the domain points of a quadratic spline.
(Understanding the picture and the argument on this page
requires familiarity with
the Bernstein-Bézier form
of a bivariate polynomial.) The gray shaded triangles are
actually four of the quadrilaterals that determine
differentiability across the edges. The quadrilaterals have
degenerated into triangles because of the special location
of the singular vertex. By contrast, the Figure "S12
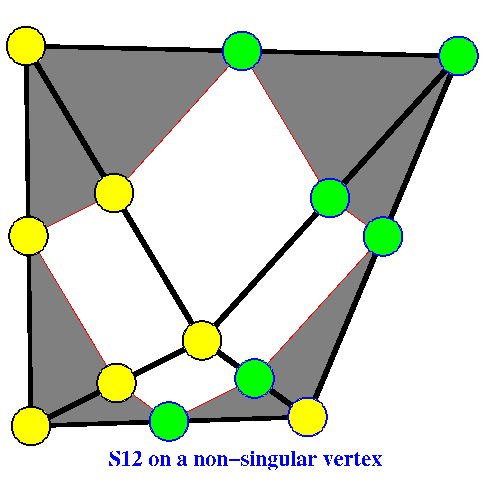
on a non-singular vertex" shows the generic case where
the quadrilaterals are true quadrilaterals.
The dimension of S1d, where d>1, increases by one when an interior vertex of degree 4 becomes singular. To see this it is sufficient to consider the case d=2 since for larger values of d the same arguments apply to the disk of radius 2 of domain points around the interior vertex.
First consider the generic case. Yellow domain points mean that we specify the corresponding Bézier ordinates arbitrarily. Thus we specify a quadratic polynomial on the west triangle. The smoothness conditions imply the values of all Bézier ordinates corresponding to domain points marked green, except the two points on the eastern edge. Now also specify the south east point. The smoothness condition across the southeast edge implies the Bézier ordinate at the center of the eastern edge, and then the smoothness condition across the northeast edge determines the value of the Bézier ordinate at the northeast vertex. Thus the dimension of S12 is 7.
The situation is more subtle in the singular case. Note that the gray quadrilaterals have degenerated into triangles. Thus the requirement that the corresponding quadrilaterals in 3-space be planar degenerates into the requirement that the three points at the base of the triangle be collinear. The fourth point of the triangle is arbitrary!
Let's begin again by specifying a quadratic polynomial p , say, on the west triangle. The smoothness conditions then imply the values of the Bézier ordinates at the green domain points, and also, because of their degenerate nature at the domain point marked cyan. Indeed, there are two smoothness conditions implying values at cyan point. Thus we have to ask if these conditions are consistent. They are because there is a piecewise polynomial function that extends p differentiably to all four triangles. It is
itself. The Bézier ordinates at the remaining points marked yellow can be specified arbitrarily! Thus the dimension of S12 increase to 8 as the interior vertex becomes singular.
An alternative view of these effects can be obtained by
considering S13 on a singular vertex, as sketched in the
Figure nearby. The
crucial assumption
of our
proposed dimension formula
is that the central smoothness conditions are linearly
independent. They are not in the case of a
singular vertex.
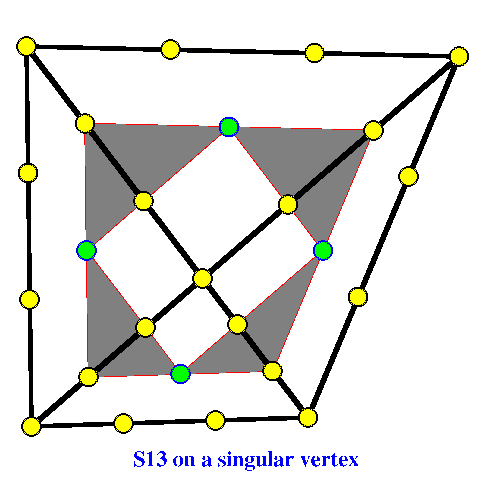
Assume that all Bézier ordinates corresponding to yellow
domain points have been assigned the value zero. Then
assigning zero to the green points will give a
differentiable function. However, there are nontrivial
solutions of this homogeneous problem, implying linear
dependence of the four central smoothness equations. To see
this consider lifting the western green control point (i.e.,
increasing the value of its Bézier ordinate). The lifting
action generates a lowering requirement on the north point,
lowering that point creates a lifting requirement on the
east point, lifting that point causes a lowering requirement
on the south point, and, finally, lowering the south point
causes a lifting requirement on the west point. Thus the
lifting action causes a lifting requirement, and because of
the geometry of the situation the action and the requirement
are identical. Thus an arbitrary value can be assigned to
the west point, and the central smoothness conditions can
still be satisfied.