


The purpose of the strange looking requirement 4 is to avoid structures like holes and "pinch points" where two triangles meet at one vertex without sharing an edge.
The following slide introduces some notation and states some
basic identities that are easily verified by induction:

The spline spaces of interest are:

Thus splines are functions that on each triangle can be represented as a bivariate polynomial of degree d, and that join smoothly of degree r across edges shared by triangles.
The Bernstein Bézier Form of a bivariate
polynomial enables us to think geometrically about algebraic
questions, in particular smoothness conditions. It is
defined in the next slide.

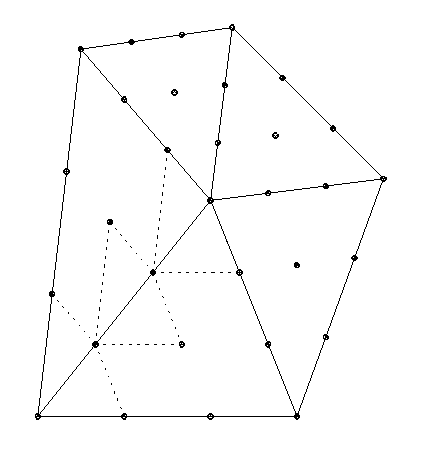
The picture nearby requires some explanation. It shows a triangulation of five triangles sharing one interior vertex. Also shown are the domain points of a spline in S13. Consider smoothness across the edge surrounded by the dashed quadrilaterals. Let's call it the edge, and the two triangles sharing it the left and the right triangle. Similarly, let's call the polynomials described on the two triangles, the left and the right polynomial, respectively.
To obtain continuity between the left and the right polynomial across the edge we consider the domain points on the edge. Even though only one set is drawn there are really two sets, one for the left and one for the right polynomial. Each set comes with its own set of Bézier ordinates. The left and the right polynomial will join continuously across the edge if and only if corresponding Bézier ordinates are equal. In other words, the two polynomials will join continuously if and only if the two sets of control points are identical.
First order differentiability conditions are a little more subtle. Assume we already have continuity and consider the three dashed quadrilaterals of domain points. Each of these corresponds to a quadrilateral in three dimensional space. Such a quadrilateral may or may not be planar. The left and right polynomial will join differentiable across the edge if and only each of these three quadrilaterals is planar. Thus each quadrilateral must lie in a plane, but the three planes need not be identical or parallel.
These results of course apply to all edges shared by two triangles. Interesting things happen at vertices. For example, consider the first ring of quadrilaterals around a vertex. By the differentiability conditions across the edges emanating from the vertex all of these quadrilaterals must lie in a plane, It turns out that this is the tangent plane of the graph of the spline at this point.
Similar statements can be obtained for higher degrees of
differentiability, but they are beyond the scope of these
pages.
[01-Nov-2023]