Department of Mathematics --- College of Science --- University of Utah

Smoothly Joining Polynomials

Splines on triangulations are functions that on each triangle can be represented as a bivariate polynomial and that join smoothly across edges shared between neighboring triangles. What does it mean to join smoothly?

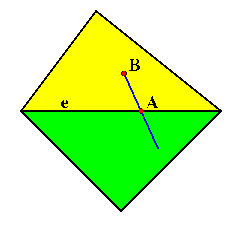
Consider the figure nearby. It shows two triangles, a yellow one and a green one, that share the edge e. Let y and g denote the polynomials on the two triangles, respectively. Let A be a point on e and B a point in the interior of the yellow triangle. A point P on the blue line connecting A and B and crossing e can be written as

P = tB + (1-t)A.

Thus, when t=0 then P is the intersection of the common edge e and the blue line. If t is (small and) positive then P lies in the yellow triangle, if it is small and negative it lies in the green triangle. Now consider the function

       y(P)  if t > 0 
s(t) = 
       g(P)  if t <= 0 

As t ranges from a negative value through zero to a positive value the point P moves along the blue line from the green triangle across e into the yellow triangle. The two polynomials join continuously if the function s is continuous at t=0 for all possible choices of A and B. More generally, they join smoothly of order r if the function s is r times differentiable, again for all choices of A and B. Following are some more technical remarks:

• Often one requires that the line through A and B be perpendicular to e. That is not necessary for the definition, however.,
• For y and g to join smoothly of order 1, say, we really require that the gradient of y and g be continuous across e . However, if y and g are already continuous across e the common edge, then their derivative in the direction of e is also continuous. Thus we need to enforce continuity of only one additional first order derivative (in any direction other than e ).
• A similar consideration applies to higher order derivatives. If we already have smoothness of degree r-1, then to obtain smoothness of degree r we only have to require that one particular directional derivative of order r across e be continuous.
• The triangles are actually not necessary for these considerations although of course they do occur in the definition of the spline space. But nothing changes if we consider two polynomials y and g defined in the half spaces on either side of the line e.
• If y and g join smoothly of some order in any interval of e then of course they join smoothly everywhere on e since a polynomial is defined uniquely by its values in an interval.