









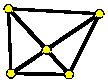
A singular vertex is an interior vertex of a triangulation where four triangles meet whose edges form two parallel pairs. In other words, the union of the triangles is a convex quadrilateral with the diagonals drawn in, as indicated in the figure nearby.
The dimension of S13 exceeds the number of vertices.
However, it is not clear that one can always interpolate to
given function values at the vertices of the triangulation.
Currently the most viable way of using S13 is to consider it
a subspace of a larger space and enforce smoothness
conditions. It is conceivable, although no such case is
known, that for some triangulations and some data the
smoothness conditions and the interpolation conditions are
inconsistent.
[01-Nov-2023]