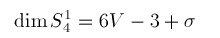The Generic Dimension of S¹₄

This page illustrates an actual proof using the Bernstein-Bézier form. It concerns the space of C¹ quartics for which a minimal determining set is constructed in reference 8 of the bibliography. There it is shown that

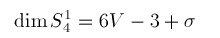(1)

where V is the number of vertices and sigma is the number of singular vertices in the triangulation.

Here we show that generically

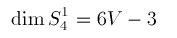(2)

The proof is by induction in the number of vertices. Clearly (2) holds for the case of just one triangle. Suppose (2) holds for V vertices and assume our triangulation T has V+1 vertices. Then consider a boundary vertex v which is such that removing its star S_v (i.e., the set of all triangles having v as a vertex) leaves a triangulation. (As an exercise you may want to show that it is always possible to find such a boundary vertex.) The triangulation remaining after removing S_v has V vertices and a minimal determining set of 6V-3 points by the induction hypotheses. We have to show that we can expand this set to a minimal determining set on all of T by adding 6 points in S_v. Since we are considering the generic case only we may assume that no pair of edges on any vertex is parallel.

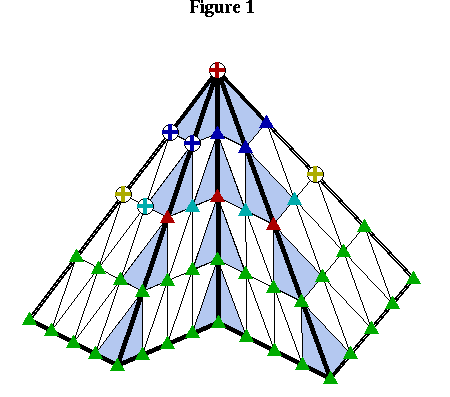
Figure 1. nearby illustrates the situation. The vertex v is indicated by the red MDS symbol (a plus sign in a circle). Bézier ordinates at the points marked with green triangles are implied by the continuity and differentiability conditions across the bottom of S_v where it joins the remaining triangles of T. Internal smoothness conditions determine Bézier ordinates at the points marked with red triangles. The points marked with yellow MDS symbols must be in the minimal determining set since they enter no smoothness conditions at all. Finally, setting the Bézier ordinates at the two points marked with blue MDS signs implies all remaining B&ezier; ordinates. There is a total of six new points in the minimal determining set. It's clear that adding these points form a determining set. To see that it is minimal it suffices to check that for each of the new points $P$ one can construct a cardinal spline where the Bézier ordinate corresponding to P is 1 and all others are zero.

A nontrivial exercise

Ask yourself how the above proof fails if some pairs of edges sharing a vertex are parallel. Then ask yourself how to fix the problem. If you are impatient read reference 8 in the bibliography.

[15-Mar-1999]