

An application of Powers is the scientific notation of numbers. The underlying basic fact is that a power of 10 whose exponent is a natural number can be easily evaluated: the exponent gives the number of zeros. For example:
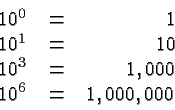
Negative exponents may be used to indicate numbers smaller than ![]() ,
e.g.,
,
e.g.,
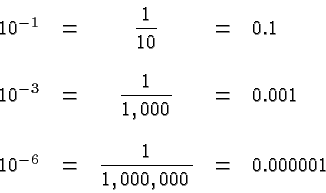
Scientific Notation is used to indicate numbers that are very large
or very small.
We write a number as a factor whose absolute
values is between ![]() and
and ![]() , and a power of
, and a power of ![]() . That power
is indicated either by an actual power with an exponent, or the letter
. That power
is indicated either by an actual power with an exponent, or the letter
![]() followed by just the exponent.
followed by just the exponent.
Here are some examples:
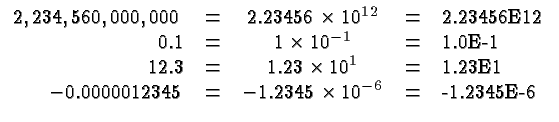
A light year is the distance covered at the speed of light in one year. It equals approximately
The radius of the visible universe is (very) roughly 10 billion light
years or
![]() miles. It contains (again very roughly)
miles. It contains (again very roughly) ![]() atoms.
atoms.


So for example, one km is 1,000 meters, and a cm is one hundredth of a meter. (A meter is 3.28 feet.)
However, computers use ![]() as the base of its number system. So in
the computer industry kilo means multiply with
as the base of its number system. So in
the computer industry kilo means multiply with
![]() ,
mega means multiply with
,
mega means multiply with
![]() , and giga
means multiply with
, and giga
means multiply with
![]() You can look at this
either as getting more in your computer than you asked for, or the
computer industry hopelessly and ruthlessly confusing Math 1010 students.
You can look at this
either as getting more in your computer than you asked for, or the
computer industry hopelessly and ruthlessly confusing Math 1010 students.