Department of Mathematics --- College of Science --- University of Utah

Mathematics 1010 online

Scientific Notation

An application of Powers is the scientific notation of numbers. The underlying basic fact is that a power of 10 whose exponent is a natural number can be easily evaluated: the exponent gives the number of zeros. For example:

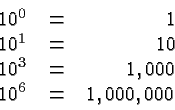
$\begin{displaymath} \begin{array}{rcr} 10^0 &=& 1 \\ 10^1 &=& 10 \\ 10^3 &=& 1,000 \\ 10^6 &=& 1,000,000 \\ \end{array} \end{displaymath}$

Negative exponents may be used to indicate numbers smaller than , e.g.,

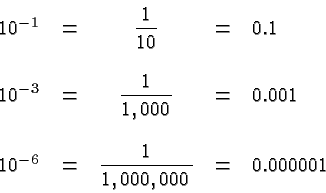
$\begin{displaymath} \begin{array}{rcccl} 10^{-1} &=& \displaystyle\frac{1}{10} &... ...\displaystyle\frac{1}{1,000,000} &=& 0.000001 \\ \end{array} \end{displaymath}$

Scientific Notation is used to indicate numbers that are very large or very small. We write a number as a factor whose absolute values is between and , and a power of . That power is indicated either by an actual power with an exponent, or the letter followed by just the exponent.

Here are some examples:

First some numbers:

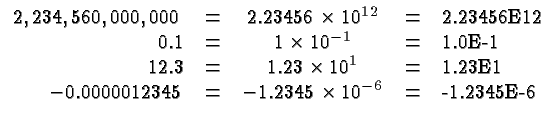
$\displaystyle \begin{array}{rcccl} 2,234,560,000,000 &=& 2.23456 \times 10^{12}... ... -0.0000012345 &=& -1.2345\times 10^{-6} &=& \hbox{-1.2345E-6} \\ \end{array}$
A light year is the distance covered at the speed of light in one year. It equals approximately

$\displaystyle 5,880,000,000,000 = 5.88\times 10^{12} = 5.88E12 \quad\hbox{miles.}$
The radius of the visible universe is (very) roughly 10 billion light years or miles. It contains (again very roughly) atoms.

It is worthwhile to know the words that describe the powers of 10, as in this table:

$\begin{displaymath} \begin{array}{rcl} 10^3 & =& \hbox{one thousand} \\ 10^6 &... ...llion} \\ 10^{30} & =& \hbox{one nonillion} \\ \end{array} \end{displaymath}$

The federal deficit is about $\char 36 5E12$ , or $5 trillion. It will be a long time before we run out of words that describe it.

A googol is a followed by a 100 zeros, or $10^{100} = 1E100$ . A googolplex is a followed by a googol zeros, or $10^{\left(10^{100}\right)}$ . In scientific notation a googolplex is

$\displaystyle 1.0E10000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000$
My son, who likes to exaggerate, once told me that my age measured in years equals a googolplex plexed a googolplex times. You ponder that number! Despite its size most natural numbers are bigger, in fact, only finitely many are smaller.

The decimal system uses prefixes to indicate factors that are powers of 10, as follows:

$\begin{displaymath} \begin{array}{rcl} \hbox{prefix} & \hbox{Symbol} &\hbox{Fact... ...& n & 10^{-9} \\ \hbox{pico} & p & 10^{-12} \\ \end{array} \end{displaymath}$

So for example, one km is 1,000 meters, and a cm is one hundredth of a meter. (A meter is 3.28 feet.)

However, computers use as the base of its number system. So in the computer industry kilo means multiply with $2^{10}=1024$ , mega means multiply with $2^{20} = 1,048,576$ , and giga means multiply with $2^{30} = 1,073,741,824.$ You can look at this either as getting more in your computer than you asked for, or the computer industry hopelessly and ruthlessly confusing Math 1010 students.