Department of Mathematics --- College of Science --- University of Utah

Mathematics 1010 online

More on Quadratic Equations

Quadratic equations don't always look like quadratic equations. On this page we'll discuss several examples of equations that can be converted to a quadratic equation, despite initial appearances.

Whenever you solve an equation, remember to check your answers by substituting them in the originals equation. I'll assume you'll do that and won't mention it specifically in these examples.

• Example 1. Rational Equations. Consider the equation
  
  To get rid of the ratios we simply multiply with both denominators on both sides:
  
  Canceling common factors in numerator and denominator gives
  
  which simplifies to
  
  Subtracting the right side from the left gives a quadratic equation in standard form:
  
  We solve this equation as usual by completing the square:
  
  which tells us that or .

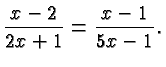
• Example 2. Changing the Variable. The equation

  
  looks like a complicated radical equation, but it becomes much more benign if we think of the variable not as but as the square root of . Indeed, let's give it a name:
  
  Another way of putting this is to say that Then our equation becomes
  
  This ordinary quadratic equation has the solutions and . Hence the solutions of the original equation are
  

• Example 3. More on changing the variable. The equation

  
  is quartic and has four solutions. However, it is really a quadratic equation in disguise. Setting
  
  gives the ordinary quadratic equation
  
  which has the two solutions
  
  Thus the solutions of the original equation are: