

Working with Lines
This page contains examples of common calculations involving
the graphs and equations of lines .
1. Given the General Form, Find Everything
Consider the line defined by
To find the 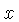 intercept we set
intercept we set 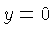 and solve the resulting
equation:
and solve the resulting
equation:
The
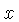 -intercept is
-intercept is 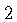 . Similarly, to find the
. Similarly, to find the 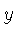 -intercept we
set
-intercept we
set 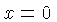 and solve the resulting equation:
The
and solve the resulting equation:
The 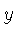 -intercept is
-intercept is
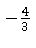 . The
. The 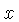 and
and 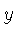 -intercepts also gives us two
points, namely
-intercepts also gives us two
points, namely 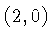 and
and 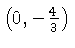 . Two
points give us the slope:
We
already know the
. Two
points give us the slope:
We
already know the 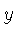 -intercept so the slope-intercept form of the
line is
Of course, we can also find
that form by solving the equation
-intercept so the slope-intercept form of the
line is
Of course, we can also find
that form by solving the equation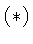 directly for
directly for 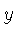 . Subtract
. Subtract
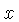 on both sides and divide by negative
on both sides and divide by negative 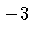 to get the same
equation.
to get the same
equation.
The line is shown in the following Figure:
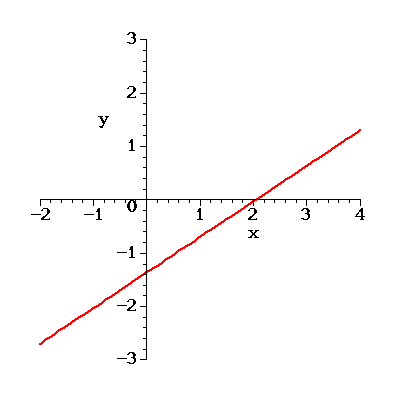
2. Given Two Points, Find the Line
Suppose we know that our line contains the points 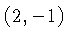 and
and 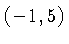 .
Then we can immediately compute the slope:
.
Then we can immediately compute the slope:
Thus the slope -intercept form of our line is
where we not yet know 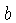 . However, we know two points on the line.
Either can be used to compute
. However, we know two points on the line.
Either can be used to compute 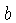 . In fact, it is a good idea to use both points to check our calculation. (Always check your answers!). Using the point
. In fact, it is a good idea to use both points to check our calculation. (Always check your answers!). Using the point
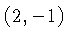 we obtain the equation
The other point,
we obtain the equation
The other point, 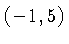 , gives the same value of
, gives the same value of 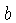 :
The following Figure shows the required line:
:
The following Figure shows the required line:

3. Given Two Intercepts, Find the Line
Two intercepts are a special case of two points. For example, suppose
the 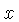 intercept is
intercept is 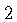 and the
and the 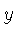 intercept is
intercept is 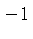 . Then
we know that the graph of the line contains the points
. Then
we know that the graph of the line contains the points 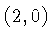 and
and
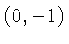 . The slope is
. The slope is
The "intercept" in the slope-intercept form of the line is the 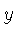 intercept, thus the slope intercept form of this particular line is
This particular line is shown in the following
Figure:
intercept, thus the slope intercept form of this particular line is
This particular line is shown in the following
Figure:
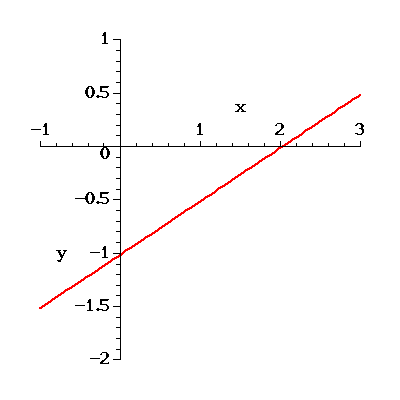
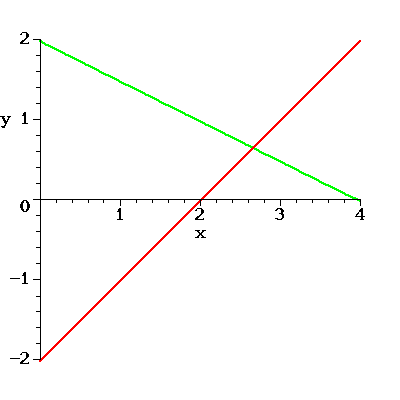
4. Finding the Intersection of Two Lines
The key here is the fact that the coordinates of the intersection
satisfy the equations of both lines. Suppose we have the lines
Both equations hold for the intersection 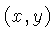 . Since the
. Since the 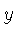 values are equal we obtain the equation
Adding
values are equal we obtain the equation
Adding 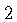 and
and 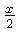 on both sides gives
Dividing by
on both sides gives
Dividing by 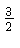 gives
To obtain
gives
To obtain 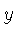 we substitute this value of
we substitute this value of 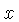 in one of the equations, and check that we get the same answer by substituting in the other equation.
We get
in one of the equations, and check that we get the same answer by substituting in the other equation.
We get
So the intersection point is 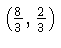 . The following Figure shows both lines and the intersection:
. The following Figure shows both lines and the intersection:
5. Finding a Perpendicular Line
Suppose we are given a line 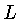 and a point
and a point 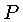 . We want an
equation of the line through
. We want an
equation of the line through 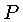 and perpendicular to
and perpendicular to 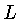 . The
key fact here is that lines are perpendicular if their slopes are
negative reciprocals of each other. For example, suppose
. The
key fact here is that lines are perpendicular if their slopes are
negative reciprocals of each other. For example, suppose 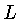 has
the equation
has
the equation
and we want to find the equation of the
perpendicular line that passes through the point 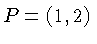 . The
slope of that line is the negative reciprocal of
. The
slope of that line is the negative reciprocal of 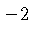 , i.e.,
, i.e.,
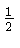 and so the perpendicular line has the equation
where we need to determine
and so the perpendicular line has the equation
where we need to determine 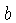 . Since
. Since
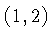 lies on that perpendicular line we have the equation
and so
lies on that perpendicular line we have the equation
and so 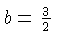 . The equation of the
perpendicular line is
The
following Figure shows both lines:
. The equation of the
perpendicular line is
The
following Figure shows both lines:
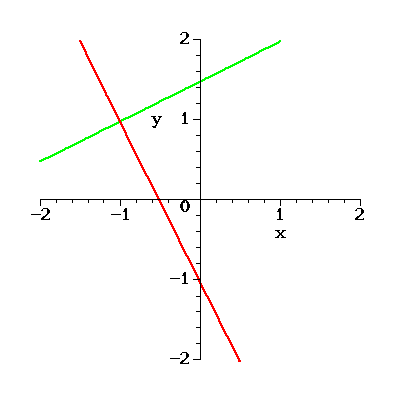
As described above, we can also compute their
intersection. Solving
gives
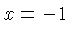 and substituting in one or both of the equations gives
and substituting in one or both of the equations gives
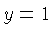 . The two lines intersect in the point
. The two lines intersect in the point 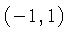 . Some of
the home work problems ask to compute the distance of
. Some of
the home work problems ask to compute the distance of 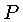 from the
intersection point, in this case that distance is
from the
intersection point, in this case that distance is
6. Finding the Distance between a Point and a Line
The procedure is outlined in the preceding paragraph. Here is a n
outline. Suppose the line is 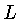 and the point is
and the point is 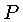 .
.
- Find an equation of the line
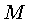 through
through 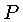 , and perpendicular to
, and perpendicular to 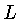 .
.
- Compute the intersection
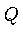 of
of 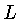 and
and 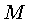 .
.
- Compute the Distance between
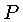 and
and 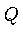 .
.


![]() intercept we set
intercept we set ![]() and solve the resulting
equation:
and solve the resulting
equation: 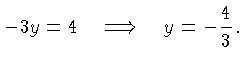
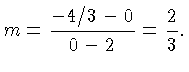
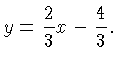
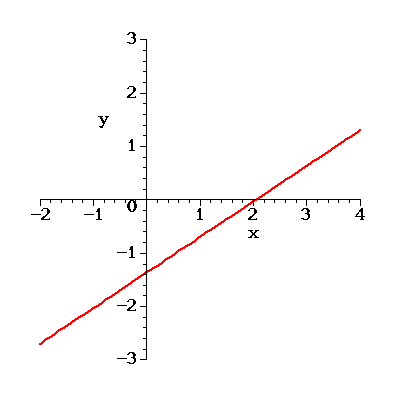
![]() and
and ![]() .
Then we can immediately compute the slope:
.
Then we can immediately compute the slope:
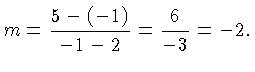

![]() intercept is
intercept is ![]() and the
and the ![]() intercept is
intercept is ![]() . Then
we know that the graph of the line contains the points
. Then
we know that the graph of the line contains the points ![]() and
and
![]() . The slope is
. The slope is 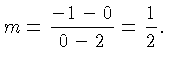
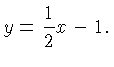
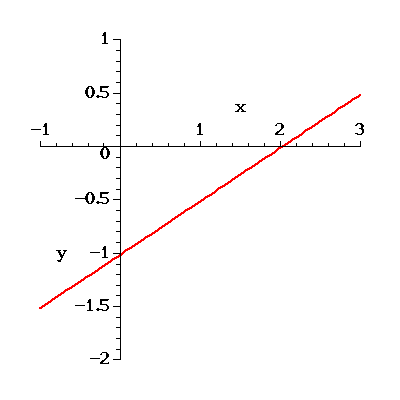
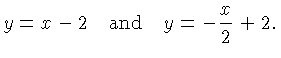
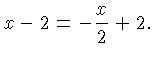
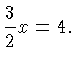
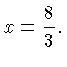
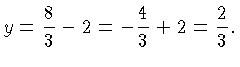
![]() . The following Figure shows both lines and the intersection:
. The following Figure shows both lines and the intersection:

![]() and a point
and a point ![]() . We want an
equation of the line through
. We want an
equation of the line through ![]() and perpendicular to
and perpendicular to ![]() . The
key fact here is that lines are perpendicular if their slopes are
negative reciprocals of each other. For example, suppose
. The
key fact here is that lines are perpendicular if their slopes are
negative reciprocals of each other. For example, suppose ![]() has
the equation
has
the equation 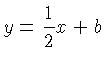
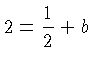
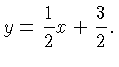
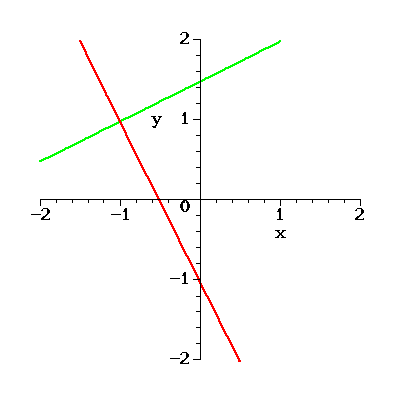
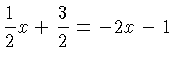
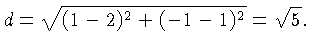
![]() and the point is
and the point is ![]() .
.