

Consider a right triangle whose two short sides have a length of ![]() foot each. By the
Pythagorean Theorem the long side has a length of
foot each. By the
Pythagorean Theorem the long side has a length of ![]() feet. It turns out that
feet. It turns out that ![]() is not a
rational number .
is not a
rational number .
This remarkable fact can be seen by a classic argument usually attributed to
Eudoxus of Cnidus (approx. 406-355BC).
We assume that ![]() is in fact rational and then derive a
contradiction. Since there are no contradictions in mathematics our
assumption must be false and so
is in fact rational and then derive a
contradiction. Since there are no contradictions in mathematics our
assumption must be false and so ![]() must be irrational.
must be irrational.
So let us suppose that ![]() can be written as a ratio of two
integers
can be written as a ratio of two
integers ![]() and
and ![]() :
:
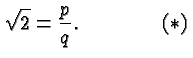
We start with the equation ![]() . Squaring on both sides gives
. Squaring on both sides gives
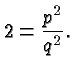
Because of the factor ![]() on the left side, the right side, i.e.,
on the left side, the right side, i.e.,
![]() , must be even. For this to be true,
, must be even. For this to be true, ![]() itself must be
even. If
itself must be
even. If ![]() is even then
is even then ![]() is divisible by
is divisible by ![]() . Hence
. Hence
![]() is also divisible by
is also divisible by ![]() which means that
which means that ![]() must be
even. That implies in turn that
must be
even. That implies in turn that ![]() must be even. Thus
must be even. Thus ![]() and
and
![]() must be both even, which contradicts our (legitimate)
assumption that
must be both even, which contradicts our (legitimate)
assumption that ![]() and
and ![]() have no factor in common. Our
(doubtful) assumption that
have no factor in common. Our
(doubtful) assumption that ![]() is rational therefore can't be
true -- the square root of
is rational therefore can't be
true -- the square root of ![]() is not a rational number.
is not a rational number.
The following facts regarding irrational numbers are beyond the scope of this class, but you can read about them in the book "What is Mathematics" by Courant Robbins, or I would be pleased to tell you more if you are interested: