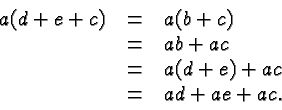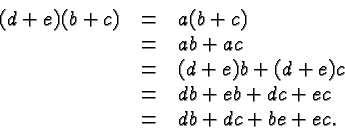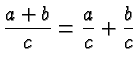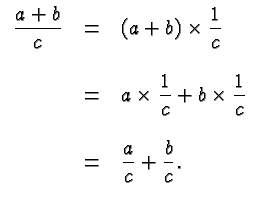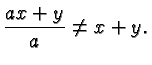Department of Mathematics --- College of Science --- University of Utah

Mathematics 1010 online

The Distributive Law

Quite likely the greatest source of errors in Intermediate Algebra is the Distributive Law

$\displaystyle a(b+c ) = ab + ac.$

Since the commutative Law

$\displaystyle uv = vu$

also holds we have the alternative version

$\displaystyle (b+c)a = ba + ca = ab + ac.$

There are several subtleties in this law, any of which can give rise to errors.

You should work through all of the following items and make sure you understand what they say. If it helps assign values to the variables, such as

$\displaystyle a=2, \quad b=3, \quad c= 5.$

Also consider the special cases that some of the variables are

, or

, or negative.

There is nothing magical about the letters , and .
It's the pattern that matters: you multiply a sum with a factor by multiplying each term in the sum with that factor.
A more general version of the Distributive Law is that the product of two sums is the sum of all possible products of one term from the first sum and one term for the second sum. For example

$\displaystyle (a+b+c)(d+e+f) = ad+ae+af+bd+be+bf+cd+ce+cf.$
If you multiply a sum of 20 terms with a sum of 30 terms you get a sum of 600 terms.
The variables , and may be algebraic expressions. For example, might equal in which case the Distributive Law becomes

$\begin{displaymath} \begin{array}{rcl} a(d+e+c) &=& a(b+c) \\ &=& ab + ac \\ &=& a(d+e) + ac \\ &=& ad + ae + ac.\\ \end{array} \end{displaymath}$
Or might be a sum, e.g., in which case we obtain

$\begin{displaymath} \begin{array}{rcl} (d+e)(b+c)&=& a(b+c) \\ &=& ab + ac \\ &=... ...\ &=& db + eb +dc + ec \\ &=& db + dc +be + ec.\\ \end{array} \end{displaymath}$
The formula

$\displaystyle (d+e)(b+c) = db + dc + be + ec$
is sometimes called the principle of FOIL (first-outer-inner-last) but that's just a special case of the Distributive Law. It does not pay to commit such special cases to memory.
Since division is equivalent to multiplication with the reciprocal, division is just a special case of multiplication. Hence a formula such as

$\displaystyle \frac{a+b}{c} = \frac{a}{c} + \frac{b}{c}$
is a special case of the distributive law because

$\displaystyle \begin{array}{rcl} \displaystyle \frac{a+b}{c} &=& \displaystyle ... ...frac{1}{c} \\ \\ &=& \displaystyle \frac{a}{c} + \frac{b}{c}. \\ \\ \end{array}$
It is tempting to omit the parentheses but in general

$\displaystyle a(b+c) \neq ab+c.$
Similarly, when canceling common factors in a ratio one has to make sure that the factor is in fact a factor in each term of both the numerator and denominator. For example

$\displaystyle \frac{ax+y}{a} \neq x+y.$
A common fallacy is to think that you square a sum by squaring each term. You don't!

$\displaystyle (a+b)^2 \neq a^2 + b^2.$
Instead

$\displaystyle (a+b)^2 = (a+b)(a+b) = a^2 + 2ab + b^2.$
and similarly

$\displaystyle (a-b)^2 = (a-b)(a-b) = a^2 - 2ab + b^2.$
These two particular formulas are known as the first and second binomial formula, respectively. The third binomial formula is

$\displaystyle (a+b)(a-b) = a^2+ab -ab -b^2 =a^2-b^2,$
another special case of the Distributive Law.
A special case of , and being algebraic expressions is that they have a negative sign, in which case we get formulas like

$\displaystyle a(b-c) = ab-ac.$
The Distributive Law works in both directions, so you can use it to factor out a term.

$\displaystyle ab + ac = a(b+c).$
One of the factors may be and not always visible, for example

$\displaystyle a+ab = a\times 1 + b = a(1+b).$