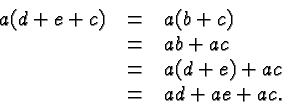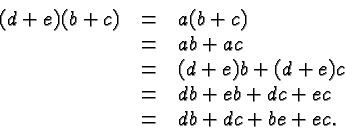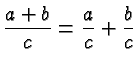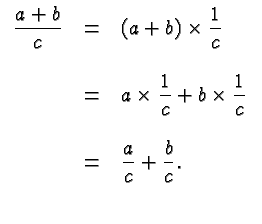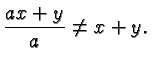Quite likely the greatest source of errors in Intermediate Algebra is the Distributive Law
There are several subtleties in this law, any of which can give rise to errors.
You should work through all of the following items and make sure you understand what they say. If it helps assign values to the variables, such as
It's the pattern that matters: you multiply a sum with a factor by multiplying each term in the sum with that factor.