

A fraction is an expression
![]() where
where ![]() and
and ![]() are
integers, and
are
integers, and ![]() . On this page we review some basic facts
about fractions. We will also see why these facts are true. The way
we'll approach the issues will be typical for approaching the kind of mathematics
you will learn in great depth in this class.
. On this page we review some basic facts
about fractions. We will also see why these facts are true. The way
we'll approach the issues will be typical for approaching the kind of mathematics
you will learn in great depth in this class.
You are familiar with these facts:
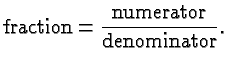
An integer can be considered a fraction with a denominator equal to 1.
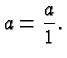
Multiplying numerator and denominator of a fraction with the same non-zero factor does not change the fraction. (In elementary school the term equivalent fractions is used, but a more mature view is that equivalent fractions denote the same real number, and hence need not be distinguished other than for clarity and simplicity.)
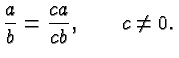
Fractions with the same denominator are added (or subtracted) by adding (or subtracting) the numerators (and keeping the denominator the same).
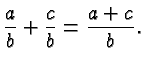
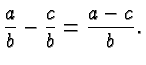
Fractions with different denominators are first turned into fractions with the same denominators, by multiplying numerators and denominators with suitable factors, and then added using the rule above.
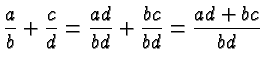
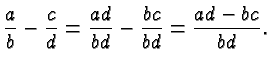
Fractions are multiplied by multiplying numerators and multiplying denominators.
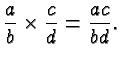
The reciprocal of a fraction is obtained by switching numerators and denominators.
Dividing a fraction by another fraction is equivalent to multiplying with the reciprocal of the second fraction.
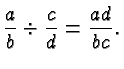
Note how we explain the addition of fractions with distinct denominators in terms of the addition of fractions with the same denominator, and the division of fractions in terms of the multiplication of fractions.
These provide instances of a principle whose statement is deceptively simple, but whose applications and implications are far reaching:
Reduce your problem to one you have solved before.
A fraction such as
![]() is simply a way to denote the
result of dividing 3 by 4. In general, a fraction
is simply a way to denote the
result of dividing 3 by 4. In general, a fraction
![]() denotes the result of dividing
denotes the result of dividing ![]() by
by ![]() . (This is true even if
. (This is true even if
![]() and
and ![]() aren't integers, an illustration of the
principle that we
make definitions in simple contexts and then generalize them so that
all relevant rules remain true. However, if
aren't integers, an illustration of the
principle that we
make definitions in simple contexts and then generalize them so that
all relevant rules remain true. However, if ![]() and
and ![]() aren't
integer then the expression
aren't
integer then the expression
![]() is called a ratio or quotient.)
is called a ratio or quotient.)
Division is defined as the solution of a multiplication problem. Thus the fraction
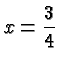
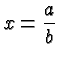
It's important to understand this basic definition, since all of the above rules can be derived from it.
We do, however, require another principle
Doing the same on both sides of an equation creates another valid equation.:
The solution ![]() of the equation
of the equation ![]() does not change if
we multiply on the left and right with the same factor
does not change if
we multiply on the left and right with the same factor ![]() to obtain
the equivalent equation
to obtain
the equivalent equation ![]() .
We have as an immediate consequence the above identity:
.
We have as an immediate consequence the above identity:
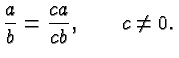
Let's suppose we are given two fractions
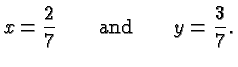
As we discussed, these fractions are defined by the equations
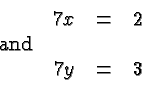
We now add ![]() on both sides of the first equation. This will give
another valid equation. However, on the left we will not use the
number
on both sides of the first equation. This will give
another valid equation. However, on the left we will not use the
number ![]() , but instead the expression
, but instead the expression ![]() . We can do this because
the second equation asserts that
. We can do this because
the second equation asserts that ![]() equals
equals ![]() . Henceforth we will
simply say that we add the second equation to the first, but the
underlying reasoning is that we add the same thing on both sides of
the first equation, we just give it different names on the two sides
of the equation. This operation gives the new equation
. Henceforth we will
simply say that we add the second equation to the first, but the
underlying reasoning is that we add the same thing on both sides of
the first equation, we just give it different names on the two sides
of the equation. This operation gives the new equation
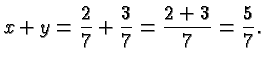
It is clear how this argument applies to general fractions with the same denominator, and to the subtraction (as opposed to the addition) of fractions.
When adding two fractions like
![]() and
and
![]() we
first convert them to fractions with the same denominator by applying
rule number 3 above. Thus we have to find a common
denominator. As a practical matter, the smaller the denominator the
easier it is to manipulate the numbers, and therefore we like to use
the least common denominator. However, the product of the two
denominators always works, and it is often, like in this case, also the
least common denominator.
So in this example we use
we
first convert them to fractions with the same denominator by applying
rule number 3 above. Thus we have to find a common
denominator. As a practical matter, the smaller the denominator the
easier it is to manipulate the numbers, and therefore we like to use
the least common denominator. However, the product of the two
denominators always works, and it is often, like in this case, also the
least common denominator.
So in this example we use
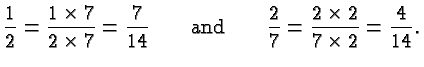
Thus
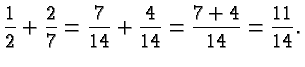
Suppose we are given two fractions
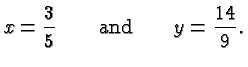
This means ![]() and
and ![]() satisfy the equations
satisfy the equations
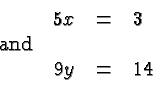
Proceeding as above, and multiplying on both sides of the first
equation with ![]() , but calling it
, but calling it ![]() on the left, we obtain
on the left, we obtain
This can be rewritten as
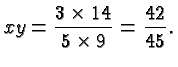
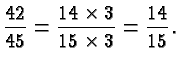
Suppose we want to divide the same fractions as above. So we ask what is
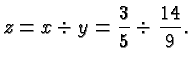
Division is the inverse process of multiplication, so ![]() satisfies
the equation
satisfies
the equation
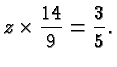
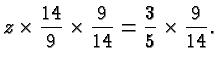
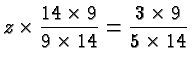
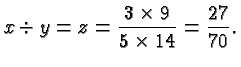
The relevance of all this is that a common denominator of two fractions is a common multiple of the two denominators, and the least common denominator is the least common multiple of the two denominators.
The least common multiple LCM and the greatest common factor GCF of two numbers m and n are related by the fact
LCM = m*n/GCFFor example, the GCF of 4 and 6 is 2, their least common multiple is 12 and indeed
12 = 4*6/2
Think about this and send me your explanation of this fact!
Mixed Numbers are fractions written as a natural number plus a
fraction where the denominator is greater than the numerator. For
example,
Mixed numbers are popular because the integer part gives an
indication of their size, but otherwise they have little to recommend
them. They form an exception (the only exception) to the rule that a
missing operator means multiplication, and they make the arithmetic
operations harder to carry out. We will not use them in this class
and I recommend you ignore their existence.
For large numerators and denominators the most practical way of
finding common factors is the Euclidean
Algorithm described elsewhere, but for many small factors there
are simple rules available. They are listed in the following Table.
It's a good exercise to think about why these rules hold. If you
can't figured it out drop me a note!
Mixed Numbers
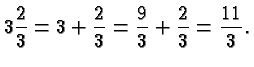
Divisibility Rules
When working with fractions it is convenient to eliminate common
factors in numerator and denominator, to keep numerators and
denominators as small as possible.
| Factor | Rule | Examples |
| 2 | last digit is 0, 2, 4, 6, or 8 | 2, or 127174 |
| 3 | sum of digits is divisible by 3 | 111 (s.o.d. = 1+1+1 = 3.) 111= 3*37, or 212,319,231 (s.o.d. = 24), 212,319,231 = 3*70,773,077. |
| 4 | the last two digits form a number that is divisible by 4. | 1,232, or 12,135,432,196 |
| 5 | last digit is 0, or 5 | 58,213,475 |
| 6 | Apply tests for 2 and 3 | 228, or 5,832 |
| 7 | there is no good test, divide by 7 | 2,443 |
| 8 | the last three digits form a number that is divisible by 8. | 25,432, or 2,942,600 |
| 9 | sum of digits is divisible by 9 | 111 (s.o.d. = 3+3+3 =9.) 333= 9*37. 242,319,231 (s.o.d. = 27), or 242,319,231 = 9*26,924,359. |
| 10 | last digit is 0 | 20, or 123,456,780 |
There is also a well known rule for divisibility by 11. You form one sum by adding the first, third, fifth, etc. digit, and another by adding the second, fourth, sixth, etc. The number is divisible by 11 is the difference of the sums is. For example, suppose we want to check
m = 5,123,456,789.
The sum of the digits in the odd numbered positions is 9+7+5+3+1 = 25. The sum of the digits in the even numbered positions is 8+6+4+2+5 = 25. The difference is 25-25 = 0. 0 is divisible by 11, and so is m. Indeed,
5,123,456,789 = 11*465,768,799.
Check it out!