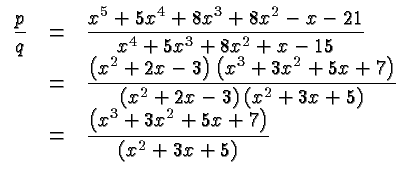Department of Mathematics --- College of Science --- University of Utah

Mathematics 1010 online

The Euclidean Algorithm


Euclid of Alexandria lived during the third century BC. The Algorithm named after him let's you find the greatest common factor of two natural numbers or two polynomials .

Division of polynomials

Polynomials can be divided mechanically by long division, much like numbers can be divided. Numbers represented in decimal form are sums of powers of 10. Polynomial expressions similarly are sums of powers of the variable (let's say $ x $). There are two main differences:

Let's illustrate the division process with a couple of examples.

We can easily check that

$\displaystyle x^2 + 3x + 4 = (x+1)(x+2) + 2.\qquad(1) $

This can be rewritten as

$\displaystyle \left(x^2 + 3 x + 4\right) \div (x+1) = x+2 \quad\hbox{\bf R}\quad 2 \qquad(2) $

The symbol $ \quad\hbox{\bf R}\quad $ stands for remainder. The ingredients of this expression have the following names:

The equation $ (2) $ can be rewritten alternatively, and equivalently, as:

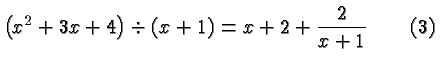
$\displaystyle \left(x^2 + 3 x + 4\right) \div (x+1) = x+2 + \frac{2}{ x+1} \qquad(3) $

Thus the equations $ (1) $, $ (2) $, and $ (3) $ are all equivalent.

To illustrate the terminology let's rewrite $ (2) $ with the words replacing the expressions:

$\displaystyle \hbox{dividend} \div \hbox{divisor} = \hbox{quotient} \quad\hbox{\bf R}\quad \hbox{remainder} $

If the remainder is zero then we say the divisor divides the dividend evenly.

Given a dividend and a divisor, the quotient and the remainder can be found by long division. For example, the division in $ (1) $-$ (3) $ can be written as:

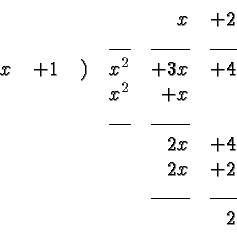
\begin{displaymath} \begin {array}{rrrrrr} & & & & x & +2 \\ & & & \leaders\hr... ...e\hfill & \leaders\hrule\hfill \\ & & & & &2 \\ \end{array} \end{displaymath}

Notes

Here is a more complicated example, Some of the coefficients of the dividend and the quotient are zero. They are given here explicitly, but with practice you may just leave these spaces blank.

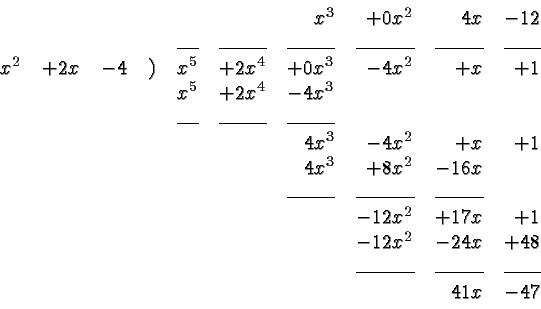
\begin{displaymath} \begin{array}{rrrrrrrrrrr} & & & & & & x^3 & + 0 x^2& 4 x &... ...eaders\hrule\hfill & \\ &&&&&& & & 41 x &-47 \\ \end{array} \end{displaymath}

Thus

$\displaystyle \left(x^5+2x^4-4x^2+x+1\right)\div\left(x^2+2x-4\right) = x^3 + 4x -12 \quad\hbox{\bf R}\quad 41x-47. $

The greatest common factor of two natural numbers

Let's say we want to find the greatest common factor of two natural numbers $ m $ and $ n $, and let's suppose $ m $ is the larger of the two, i.e., $ m > n $.

The Euclidean Algorithm proceeds by dividing $ m $ by $ n $, with remainder, then dividing the divisor by the remainder, and repeating this process until the remainder is zero. The greatest common factor of $ m $ and $ n $ is the last divisor. (Notice that at no point do you pay attention to the current quotient.)

The following examples illustrate the process. Suppose we want to find the greatest common factor of $ 110 $ and $ 143 $. We have

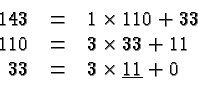
\begin{displaymath} \begin{array}{rcl} 143 &=& 1 \times 110 + 33 \\ 110 &=& ... ... + 11 \\ 33 &=& 3\times \underline{11} + 0 \\ \end{array} \end{displaymath}

The last remainder is zero, the last divisor is $ 11 $, and so $ 11 $ is the greatest common factor of 110 and 143. Indeed,

$\displaystyle 110 = 10 \times 11 \qquad\hbox{and}\qquad 143 = 13 \times 11. $

Clearly, 11 is a common factor, and there is no greater common factor.

Here is another example. The greatest common factor of $ 72 $ and $ 102 $ is $ 6 $. We have:

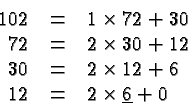
\begin{displaymath} \begin{array}{rcl} 102 &=& 1 \times 72 + 30 \\ 72 &=& 2 ... ...2 + 6 \\ 12 &=& 2 \times \underline{6} + 0 \\ \end{array} \end{displaymath}

Indeed,

$\displaystyle 102 = 6 \times 17 \qquad\hbox{and}\qquad 72 = 6 \times 12. $

There are two ingredients that make the Euclidean Algorithm work:

Of course, we could have solved the problems in these particular examples by listing all the factors of the numbers involved and finding the largest. Another technique is to find all the prime factors and see which ones are common to the numbers. Those techniques work fine for the small numbers. The power of the Euclidean Algorithm becomes apparent when the factors aren't obvious, i.e., when we have large numbers. Consider this example: Let

$\displaystyle m = 37894060279 \qquad\hbox{and}\qquad n = 18272779829. $

Factoring these numbers is possible using a computer, but larger numbers (with somewhere around 200 digits) are used in security codes whose effectiveness depend on those numbers being impossible to factor with current computer equipment. While factoring large numbers -- particularly products of large prime numbers -- is difficult, finding the greatest common factor of two numbers is easy!

In this case:

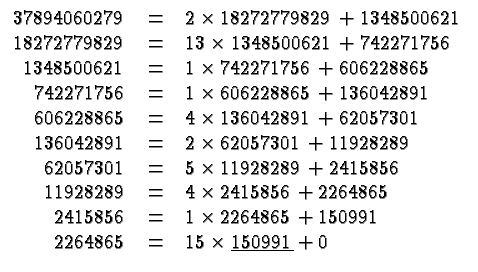
$\displaystyle \begin{array}{rcl} 37894060279 &=& 2\times 18272779829 + 13485006... ...4865 + 150991 \\ 2264865 & =& 15 \times \underline{150991} + 0\\ \end{array}$

Thus the greatest common factor of $ m=18272779829 $ and $ n=1348500621 $ is $ 150991 $. In fact, both $ m $ and $ n $ are the products of two large primes. Specifically,

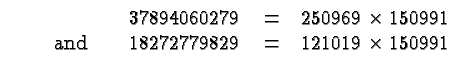
$\displaystyle \begin{array}{rcl} 37894060279 &=& 250969 \times 150991 \\ \qquad\hbox{and}\qquad 18272779829 &=& 121019 \times 150991 \\ \end{array}$

The greatest common factor of two polynomials

The same arguments as above apply to dividing polynomials with remainder. Thus the Euclidean algorithm can be used to find the ``greatest'' common factor of the numerator and denominator in a rational expression. ``Greatest'' in this context means ``highest possible degree''. A (non-zero) constant multiplying such a greatest (polynomial) factor does not matter, and we can choose it conveniently depending upon the application.

Suppose we want to find the greatest common factor of $ x^3 + 2x^2 + 2x +1 $ and $ x^3 + 3x^2 + 3x +2 $.

Using long division we see that

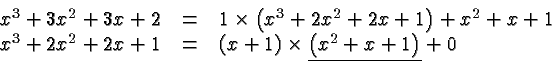
\begin{displaymath} \begin{array}{rcl} x^3 + 3x^2 + 3x +2 &=& 1 \times \left(x^... ...es \underline{\left ( x^2 + x + 1 \right)} + 0\\ \end{array} \end{displaymath}

Thus $ x^2+x+1 $ is the highest degree common factor of $ x^3 + 2x^2 + 2x +1 $ and $ x^3 + 3x^2 + 3x +2 $.

In fact, using long division again we see that

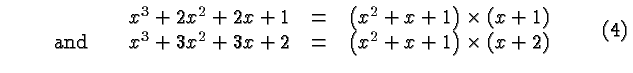
$\displaystyle \begin{array}{rcl} x^3 + 2x^2 + 2x +1 &=& \left(x^2+x+1\right) \t... ... + 3x^2 + 3x +2 &=& \left(x^2+x+1\right) \times(x+2) \\ \end{array}\qquad(4) $

Thus, for example,

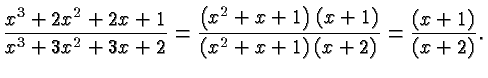
$\displaystyle \frac{x^3+2x^2+2x+1 }{ x^3+3x^2 + 3x + 2} = \frac{\left(x^2+x+1\right)(x+1) }{ \left(x^2+x+1\right)(x+2)} = \frac{(x+1) }{ (x+2)}. $

Try to do that sort of thing without the Euclidean algorithm!

Here is another example. Let

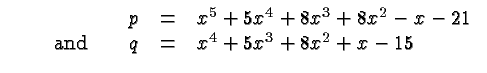
$\displaystyle \begin{array}{rcl} p &=&x^5 + 5x^4 + 8x^3 + 8x^2 - x - 21 \\ \qquad\hbox{and}\qquad q &=& x^4 + 5x^3 + 8x^2 + x - 15\\ \end{array}$

What is the greatest common factor of $ p $ and $ q $? Using long division once again we get:

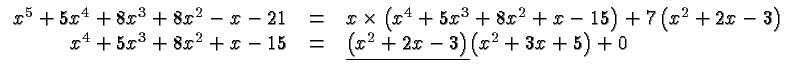
$\displaystyle \begin{array}{rcl} x^5 + 5x^4 + 8x^3 + 8x^2 - x - 21 &=& x\times ... ...line{\left(x^2 + 2x - 3\right)}{\left(x^2 + 3x + 5 \right)} + 0\\ \end{array}$

Thus the highest degree common factor of $ p $ and $ q $ is $ x^2 + 2x - 3 $ (we can ignore the constant factor 7.)

The main application of finding common factors of two polynomials is to enable to us to cancel them in the ratio of the two polynomials. In this case we obtain:

$\displaystyle \begin{array}{rcl} \displaystyle \frac{p }{ q} &=&\displaystyle \... ...left(x^3 + 3x^2 + 5x + 7\right) }{ \left(x^2 + 3x + 5\right) }\\ \end{array} $