Back to Applied Math seminar webpage

September 21
Speaker: Roberto D. Merlin, University of Michigan, Department of physics
Title: Metamaterials and the Landau-Lifshitz Permeability Argument:
Large Permittivity Begets High-Frequency Magnetism
Abstract: [in PDF] Homogeneous composites, or metamaterials, made of dielectric or metallic particles are known to show magnetic properties that contradict arguments by Landau and Lifshitz [Electrodynamics of Continuous Media (Pergamon Press, Oxford, 1960 ), p. 251] indicating that the magnetization and, thus, the permeability loses its meaning at relatively low frequencies. Here we show that these arguments do not apply to composites made of substances with κ_S = Im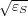 ≫ λ ∕ ℓ or n_s = Re 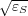~ λ ∕ ℓ (ε_S and ℓ are the complex permittivity and the characteristic length of the particles, κ_S and n_S are, respectively, the extinction coefficient and the refractive index, and λ ≫ ℓ is the vacuum wavelength). Our general analysis is supported by studies of split-rings, one of the most common constituents of electromagnetic metamaterials, and spherical inclusions. An analytical solution is given to the problem of scattering by a small and thin split ring of arbitrary permittivity. Results reveal a close relationship between ε_S and the dynamic magnetic properties of metamaterials. 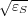For ||≪ λ ∕ a (a is the ring cross-sectional radius), the composites exhibit very weak magnetic activity, consistent with the Landau-Lifshitz argument and similar to that of molecular crystals. In contrast, large values of the permittivity lead to strong diamagnetic or paramagnetic behavior characterized by susceptibilities whose magnitude is significantly larger than that of natural substances.
The double constraint κ_S ≫ λ ∕ ℓ ≫ 1 (or, n_s ~ λ ∕ ℓ ≫ 1 if κ_S ≪ n_S) poses severe limitations for attaining magnetism at arbitrarily high frequencies. Because they have a large extinction coefficient, metals are to be favored at optical frequencies. Since ε_S ≈-ω_P² ∕ ω² for ωτ ≫ 1, the constraint becomes λ ≫ ℓ ≫ λ_P. The measured values of the permittivity for noble metals indicate that magnetism can coexist with the effective-medium condition for frequencies up to ~ 1.5 × 10¹⁴Hz (λ ~ 2.5μm)

September 23 (Wednesday 3:05pm, LCB 225, Joint with Math-Bio)
Speaker: Joyce Lin, University of Utah, Mathematics Dept.
Title: An Experimental and Mathematical Study on the Prolonged Residence Time of a Sphere Falling through Stratified Fluids at Low Reynolds Number
Abstract: Particle settling rates in strongly stratified fluids play a major role in describing a wide variety of biological and environmental phenomena, such as the vertical distribution of biomass and pollution clearing times. Applications can extend to medical issues (such as particle settling rates and stratification in centrifugal separations) and are emerging in increasingly important fields such as microfluidics. At low Reynolds number, we discover that the self-entrainment by a particle in stratified miscible fluids causes the particle to experience a significantly prolonged residence time across a density transition. We present data from an experimental investigation, emphasizing the phenomenon using a "tortoise and hare"-like race, and develop a new first-principle theory with several levels of asymptotic approximations of increasing accuracy. We test these levels through direct comparison with experimental data and assess the importance of different asymptotic terms in the model with respect to which dynamical effect needs to be predicted. Analysis of the theoretical model provides the streamlines and instantaneous stagnation points, affording some insight into the behavior of the interior of the fluid. The nondimensional form of the model is used to characterize the entire flow with only four parameters, and the impact of each of these parameters on the flow is studied numerically. The model can be further pressed into a higher Reynolds number regime, which we then compare with experimental data. A brief look is taken at the extension to free space, many-body sedimentation, and linear stratification as the starting point for future work.

September 28
Speaker: Graeme W. Milton, University of Utah, Mathematics Dept.
Title: Electromagnetic circuits
Abstract: Maxwell's equations bear a close resemblance with those of linear elastodynamics. So a natural question to ask is: what is the electromagnetic analog of a mass-spring network in elastodynamics? We assume the frequency is fixed and construct such an analog, which we call an electromagnetic circuit. By interchanging the roles of epsilon and mu we also obtain magnetoelectric circuits. Then one can join electromagnetic and magnetoelectric circuits to obtain hybrid circuits. Their response is measured in terms of the electric or magnetic field along or across the terminal edges of the circuit. This response is governed by a symmetric matrix with negative semidefinite imaginary part. Conversely given any such matrix a recipe is given for constructing a hybrid circuit which has that matrix as its response matrix. This is joint work with Pierre Seppecher.

October 5
Speaker: Andrej Cherkaev, University of Utah, Mathematics Dept.
Title: Composites on lattices
Abstract: The talk describes a joint paper with Enrico Rogora. We work out a finite-difference definition of a heterogeneous conducting material, define a composite on lattices, effective properties and their bounds, conductivity of lattice laminates, and introduce the monad - a smallest material piece that generates a lattice composite. We present the translation bounds for lattice laminates.

October 19
Speaker: Michael H. Bartl, University of Utah, Chemistry dept.
Title: Bioinspired Photonic Band Gap Crystals at Visible Frequencies
Abstract: The strikingly colorful world of insects is in large part the result of optical interference produced by the interaction of light with precisely ordered, periodic bio-polymeric structures, incorporated into their exoskeletons. Such structural colors have recently gained tremendous interest for the use as photonic crystals with promising potential for energy and information technology applications. While our current photonic engineering capabilities at visible wavelengths are rather limited, biological systems have evolved to create the most complex photonic architectures - structures that are still far out of our synthetic reach. For example, we discovered recently that the brilliant coloration of several beetles is the result of photonic structures with a diamond-based lattice - one of the most efficient photonic architectures. I will also present bio-templating fabrication routes that take advantage of the synergistic combination of photonic engineering in biology with sol-gel chemistry-based materials synthesis. Using this approach, we create high-dielectric three-dimensional photonic crystals with a variety of lattice geometries and band gaps at visible frequencies. In order to evaluate the properties of these novel photonic architectures, we apply a range of structural and optical characterization tools, including multi-directional optical reflectance micro-spectroscopy, optical and electron microscopy as well as photonic band structure calculations.

October 26
Speaker: Guy Baruch, Tel Aviv University
Title: Numerical solution of the nonlinear Helmholtz equation
Abstract: The nonlinear Helmholtz equation models the propagation of intense laser beams in Kerr media such as water, silica and air. It is a semilinear elliptic equation which requires non-selfadjoint radiation boundary-conditions, and remains unsolved in many configurations.
Its commonly-used parabolic approximation, the nonlinear Schrodinger equation (NLS), is known to possess singular solutions. We therefore consider the question, which has been open since the 1960s: Do nonlinear Helmholtz solutions exists, under conditions for which the NLS solution becomes singular ? In other words, is the singularity removed in the elliptic model ?
In this work we develop a numerical method which produces such solutions in some cases, thereby showing that the singularity is indeed removed in the elliptic equation.
We also consider the subcritical case, wherein the NLS has stable solitons. For beams whose width is comparable to the optical wavelength, the NLS model becomes invalid, and so the existence of such ``nonparaxial solitons'' requires solution of the Helmholtz model.
Numerically, we consider the case of grated material, that has material discontinuities in the direction of propagation. We develop a high-order discretization which is ``semi-compact'', i.e., compact only in the direction of propagation, that is optimal for this case.
Joint work with Gadi Fibich and Semyon Tsynkov.

November 16
Speaker: Carlos Garcia-Cervera, University of California, Santa Barbara, Mathematics Dept.
Title: Sub-linear Scaling algorithms for the study of the electronic structure of materials.
Abstract: I will discuss asymptotic-based algorithms for the study of the electronic structure of materials, in the context of density functional theory. I will illustrate the ideas using both the Kohn-Sham and orbital-free formulations. This is joint work with Weinan E (Princeton University), and Jianfeng Lu (Princeton University).

November 19 (Thursday 4:15pm, JWB 335, joint with Dept. Colloquium)
Speaker: George Papanicolaou, Stanford University
Title: Imaging with noise
Abstract: It is somewhat surprising at first that it is possible to locate a network of sensors from cross correlations of noise signals that they record. This is assuming that the speed of propagation in the ambient environment is known and that the noise sources are sufficiently diverse. If the sensor locations are known and the propagation speed is not known then it can be estimated from cross correlation information. Although a basic understanding of these possibilities had been available for some time, it is the success of recent applications in seismology that have revealed the great potential of correlation methods, passive sensors and the constructive use of ambient noise in imaging. I will introduce these ideas in an interdisciplinary, mathematical way and show that a great deal can be done with them. Things become more complicated, and a mathematically more interesting, when the ambient medium is also strongly scattering. I will end with a review of what is known so far in this case, and what might be expected.

November 20 (Friday 4:15pm, LCB 225)
Speaker: Alexander Panchenko, Washington State University
Title: Mesoscopic dynamics of large ODE systems
Abstract: The main question addressed in the talk is how, given an ODE system of particle dynamics, obtain from it the continuum equations for mesoscale spatial averages. Previously, balance equations for spatial averages (density, linear momentum, energy) were studied by Noll, Hardy, Murdoch and others. The missing ingredient in these works was closure: the equations were exact but calculation of fluxes required solving the underlying ODE system. We introduce a new quantity, generating function, that contains complete information about many conventional continuum mechanical averages, and describe how to obtain a closed form, approximate evolution equation for the generating function. The key ingredient in the derivation of this equation is a closure method based on the use of regularized deconvolutions. As an application we obtain a mesoscale kinetic equation for dense Hamiltonian systems with short range pair interactions.

November 23
Speaker: Russell Richins, University of Utah (Student talk)
Title: A Numerical Minimization Scheme for the Complex Helmholtz Equation
Abstract: The usual methods of deriving a finite element method for the Helmholtz equation result in an indefinite stiffness matrix, and the corresponding system of equations is more difficult to solve than a system with a positive definite coefficient matrix. Based on the work of Milton, Seppecher, and Bouchitté on minimization variational principles, we formulate a finite element method for solving the complex Helmholtz equation that results in a positive definite system of equations. I'll show how to treat several different boundary conditions, an example of a good preconditioner for use in conjugate gradient iterations, and an error bound for the method. Also, I'll give an example of a problem for which this method can be particularly useful.

November 30 (LCB 219)
Speaker: HwanYong Lee, University of Utah (Student talk)
Title: Analysis of electromagnetic transmission through periodic aperture arrays
Abstract: Electromagnetic wave transmission through periodic aperture arrays has been of great interest. In this talk, we consider the transmission problem through periodic hole arrays in a thin, perfect electric conductor. We derive a mathematical model for the transmission problem, obtaining an explicit linear operator equation for the tangential components of the field inside the apertures. The linear operator is regularized to ensure a stable numerical solution. And we analyze the solvability of the linear equation with a truncated and mollified operator. We then extend our problem to the case of arbitrary incoming wave by adding a Bloch condition. We also establish the conservation of energy that states the total energy of the reflected and transmitted waves is equal to the energy of the incident wave.

CANCELLED December 4 (Friday 4:15pm, LCB 225)
Speaker: Yuan Zhang, University of Utah (Student talk)
Title: Optimal structures of multiphase conducting composites
Abstract: We are looking for bounds of the energy of conducting composites made of three isotropic materials mixed in prescribed proportions, and related bounds for the anisotropic effective property tensor. One of the material is assumed to have infinity conductivity. New bounds improve the known Hashin-Shrikman bound and translation bounds found earlier. The structures (minimizing sequences are built that either realize the new bounds or approximate them.
The bounds were found using localized polyconvexity method and are geometrically independent: namely, they depend only on conductivity of the materials, their volume fractions, and the anisotropy leval of a homogeneous external field. The found optimal structures vary with the anisotropy degree of external field. We show that there are several topologically different structures and several algebraically different bounds that are optimal in different parameter domains. All the microstructures are found by the same procedure based on (i) the energy bounds and sufficient optimality conditions for fields inside each material, and (ii) the lamination technique that allows for satisfaction of these conditions.

December 7
Speaker: Benjamin Murphy, University of Utah (Student talk)
Title: Phase Transitions in Disordered Composites
Abstract: Transport in disordered composites is a problem which has attracted widespread interest in recent decades. One of the key features of these types of problems is the critical dependence of the effective transport properties on system parameters, such as volume fraction, contrast ratio of material properties, applied field strength, etc. In recent years a broad range of mathematical techniques has been developed to study phase transitions exhibited by such composites, revealing features which are virtually ubiquitous in disordered systems. I will discuss methods from statistical mechanics and random matrix theory for characterizing phase transitions in binary composites.