The purpose of this page is to summarize frequently asked questions about the
physics of skiing. The physics of skiing is a recurring topic on rsa. These
calculations and interpretations were contributed to by a number of regulars,
and some not so regulars, on rsa. The questions:
- 15.1 What's the radius of a pure carved turn?
- 15.1.1 Sidecut radius of a ski
- 15.1.2 Turning radius of a ski
- 15.1.3 Interpreting the formula
- 15.1.4 Is the a single turn radius of carved turn for a given ski?
- 15.2 Do big people go faster?
- 15.4 A simplified mathematical model of avalanches
The following book on the physics of skiing is clear and fun to read. It's
written at about the level of a freshman level physics course, and only
occassionally uses much calculus, most of which is well motivated.
- David Lind and Scott P. Sanders, The physics of skiing : skiing at the
triple point, Woodbury, N.Y., American Institute of Physics, 1997.
15.1 What's the radius of a pure carved turn?
15.1.1 Sidecut radius of a ski
The sidecut radius of a ski is a design feature of a ski found by assuming
the ski edge is an arc of a circle and determining the radius of that circle.
The following calculation descibes the radius of a circle if you know the
parameters of a sector of the circle. A sector is found by cutting off the
edge of a circle, or disc, with a straight cut that is perpendicular to the radius.
Assuming
- The ski edge forms the arc of the circle in the wedge.
- The contact line is the line running from the widest point
on the tip of the ski to the widest point on the tail of the
ski.
- The sidecut depth of the ski is the maximum height of the ski
edge measured from the contact line.

define the variables
- L = length of the contact line
- d = sidecut depth
- Rsc = sidecut radius
then the sidecut radius is
- Rsc = (L^2/4 + d^2) / (2*d)
15.1.2 Turning radius of a ski
The radius of a turn is different, and it varies as the turn is
being executed with the edge angle being used by the skier and with
the amount of reverse camber in the ski during the turn. However, it is
not too hard to calculate an approximation of the the radius of a "pure
carved turn".
Geometrically, a carved turn is the composition of two curves, the sidecut of
the ski and the deformed sidecut of the ski when its camber is reversed as it
is pressed onto the snow. To find these curve, I assumed that the carving ski
looks like a segment of a cylinder, and that the ski hill is an inclined plane.
The arc the carving ski follows is the curve at the intersection of the
cylinder and the inclined plane.
It will help you understand the formula if you'll do the following simple geometric
demonstration. Take two identical rectangular pieces of paper. With scissors,
make a large radius (shallow) sidecut on one of the long sides of piece 1. Make
shorter radius (deeper) sidecut on the corresponding side of piece 2. Now hold
each piece with the sidecut against a tabletop so that the edge of the sidecut
is in full contact with the table. Notice the decambering effect of pushing the
edge into contact with the table, and notice how changing the angle changes the
radius of the approximate cylinder.
To use this approximation, you have to calculate the radius of the
cylinder, and this involves the geometry of the ski. The approximation
I make is not too bad if you assume that the ski does not twist, but it
does calculate the radius of the carved turn when you are traversing
the hill.
To approximate the cylinder radius, I computed the distance from the
ski edge to a chord extended from the widest point on the ski tip to
the widest point on the ski tail. Then I projected that point to the
inclined plane given the inclination angle of the pressing force. If
you think about this, its easy to see that there will be a minimum
angle where this actually can be done. Thus all these calculations
should be only considered for angles above that minimum.
The variables are:
- phi = angle swept out by the sidecut of the ski, i.e.
Rsc*phi is the length of the edge from the widest
point on the tip to the widest point on the tail.
- d_rc = reverse camber distance, distance from the flat ski
to the edge when the ski is pushed into the snow
- alpha = inclination angle of the skiers leg.
- theta = inclination angle of the slope.
- Rcyl = cylinder radius.
- Rturn = turn radius
Here is the result
- d = Rsc * (1-cos(phi/2))
- d_rc = d * cot(alpha-theta)
- Rcyl = (L^2 + 4*d_rc^2)/(8*d_rc)
- Rturn = Rcyl * sin(alpha+theta)
15.1.3 Interpreting the formula
This formula is messy, but the interpretation of the formula is
interesting and easily understood. It explains, mathematically,
how a deep side cut ski carves easily. To understand this,
I'll make a comparison between two different skis.
Suppose that you want to compare carved turns between a super sidecut ski
and a regular ski when the angle of the skiers leg and the slope angle are the
equal for both skis. (Keeping the angles the same makes for a fair comparison.)
For a ski with a large side cut to carve, it must be pressed a long way down to
the snow before the edge is actually on the snow surface. In ski jargon, the ski has
a lot of reversed camber when the edge is on the snow surface. This creates a
small radius carved turn because the ski is bent into a small radius circular arc.
A ski with a small side cut cannot be pressed as far down before it comes
in contact with the snow. Consequently, it will not have as much reversed
camber. Therefore, the radius of the turn will be greater because the ski is bent
into a larger radius circular arc.
A combination of the sidecut, edge angulation and reversed camber determine
the radius of the turn. Skis with a large sidecut allow the skier to deeply reverse
camber the ski, while skis with a small side cut cannot reverse camber as much.
The combination of a large sidecut and a deep reverse camber creates short
radius carved turns.
15.1.4 Is the a single turn radius of carved turn for a given ski?
No. The carve radius depends on the relative angle between the skiers leg
and the hill. Of course, the design of some skis favor on turn radius over
another, but there isn't a "single radius of a carved turn".
15.2 Do big people go faster?
All other things taken equal, the answer is yes, but it depend on how
fast you are going.
From Patrick Chase (edited by Eyre): Let's look briefly at the free body diagram
of a skier acted upon by gravity, surface friction with the snow (modeled as
Coulombic friction) and aerodynamic body drag (neglecting skin friction). Here's
the simple free body diagram.
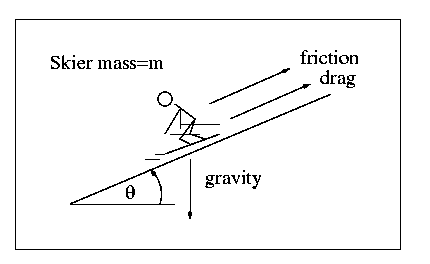
Now we can look at the individual terms:
- m*A = inertial (body) forces
- Ffriction = mu*m*g*cos(theta)
- Fdrag = (Cd*Ap*rho*V^2)/2 - drag force, opposes gravity
- Fgravity = m*g*sin(theta) - gravitational force
The force Fgravity is the gravitational force.
The inertial forces are zero if the skier is stopped or is moving
at constant velocity. Ffriction and Fdrag are the frictional and
drag forces. Both of these oppose gravity. The remaining terms
are defined as
- A - acceleration
- Cd*Ap*rho - drag coefficient times frontal area times air density
- g - gravitational acceleration
- mu - dynamic friction coefficient
- V - velocity
Balancing these forces gives the equation of motion:
- m*A = m*g*sin(theta) - mu*m*g*cos(theta) - (Cd*Ap*rho*V^2)/2
and if we divide by mass, we get
- A = g*sin(theta) - mu*g*cos(theta) - (Cd*Ap*rho*V^2)/(2*m)
The only term depending on mass is the last term, and mass appears in the
denominator. That term opposes gravity because (Cd*Ap*rho*V^2/m) is not
negative.
It should be pretty clear that the benefits (or lack thereof) of changing
mass depend upon what happens to (Cd*Ap/m) as mass is scaled upwards. It
is expected that the frontal area will increase for a more massive skier,
but it seems likely that Cd*Ap increases more slowly than m. Therefore, a
bigger skier is likely to go faster.
A few important things in this analysis have been ignored:
- A heavier skier will probably have more trouble turning, especially
if the added weight doesn't take the form of muscle in the right
places.
- The friction at the ski/snow interface was treated as coulombic.
The friction is generated in a film of meltwater in almost pure
shear. So maybe the friction model is wrong, but this does not
impact on the importance of mass.
15.2.1 If you're going fast?
The following data (from Stuart Marlatt in rec.climbing, edited by Eyre)
measures the relative effects of changing (Cd*Ap/m). While these calculations
were done for free falling objects, the effects would be similar for skiers
as (Cd*Ap/m) is changed.
To determine the terminal velocity, I used a second order Runge-Kutta to
integrate the equations of motion:
- dz/dt = v
- dV/dt = -g(z) + rho(z)*V^2*Cd(z,V)*Ap/2m
where
- z is the altitude
- V the velocity
- g is the acceleration of gravity as a function of altitude and latitude
- rho is the density of air (1962 Standand Atmosphere variation)
- Cd is the drag coefficient (as a function of altitude and velocity),
- Ap is the frontal area,
- m is the mass of our falling climber.
The fall is assumed to be from 1000m, at 41deg north. For reference
a smooth sphere with a diameter about 0.5m was used in addition to
three body positions where Cd*Ap were found from S. Hoerner's
"Fluid Dynamic Drag":
- Cd*Ap = 0.11 for an upright body, minimal frontal area
- Cd*Ap = 0.84 for a horizontal body, maximal frontal area
- Cd*Ap = 0.46 for a body in tuck position
The latter two are the most applicable to skiers. Marlatt found the
following results:
Position Time of Fall Speed at Impact
-------- ------------ ---------------
Smooth sphere 15.76s 105.8 m/s (236.7 mph)
Upright 16.44 95.3 m/s (213.2 mph)
Horizontal 28.89 37.4 m/s ( 83.7 mph)
Tuck 23.02 50.7 m/s (113.4 mph)
15.2.2 If your going slow?
In reference to the description above, the question of how much faster
does a big person go when you're going slow boils down to the following
question:
How big is (Cd*Ap*rho*V^2/2m) relative to the other terms?'
Here is the answer. Suppose that you are free falling, i.e. no
friction and theta = -90 degrees. Then you can calculate Cd from
Patrick's third equation at terminal velocity (i.e. A = 0). This
gives
- Cd = 2*g*m/(Ap*rho*(V_T^2))
for the drag coefficient where V_T is the terminal velocity. By substituting
this expression for Cd into Patrick's third equation you find
- A = g*sin(theta) - mu*g*cos(theta) - g*[V/V_T]^2
The acceleration depends on how fast the person is going relative to
his terminal velocity, i.e. on the ratio of V to V_t. The previous
section showed v_T depends on the size and shape of the person. However,
a slow skier is moving at only a small fraction of their terminal
velocity, say maybe about 1/10.
In this case, (1/10)^2 = 0.01. The sine of a 20 degree slope is 0.342,
so the acceleration due to the slope and gravity is 34 times greater than
the effects due to mass! For most practical purposes, you can ignore the
last term at small speeds.
15.3
A simplified mathematical model of avalanches

