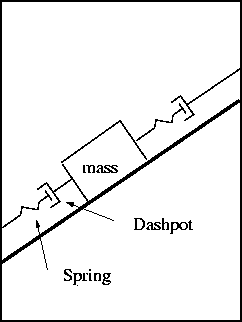
Mass-Spring-Dashpot on a wedge model of the mechanics

Using Newton's second law -- Forces on the slab are

ma = F

• Gravity
• Spring above - models tension
• Spring below - models compression
• Dashpots - model viscoelasticity

Using linear models of the springs and dashpots

mx'' + c x' + (k_u-k_d) x = mg sin(angle)

• x(t) is position
• c is the viscous damping coefficient
• k_u, k_d are the spring stiffness coefficients
  • Assumed to be constant
  • Hooke's law springs
• Resting lengths are zero (should vary slowly with time)

Solutions of the linear problem

• Equilibrium position
  x = mg sin(angle)/(k_u-k_d)

• If c > 0 then all solutions but the equilibrium solution are transient.
• Choose c big enough so the system is overdamped.

This model does not predict avalanches or depend on crystal type

• Can be used as a basis for more complex models
• Hooke's law spring will be abandoned