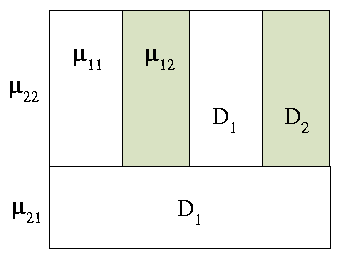
 Structure of a second rank matrix laminate
Structure of a second rank matrix laminate Matrix laminates are obtained by iterative lamination of an already built composite with the same initial materials at each step of the procedure.
 Structure of a second rank matrix laminate
Structure of a second rank matrix laminate
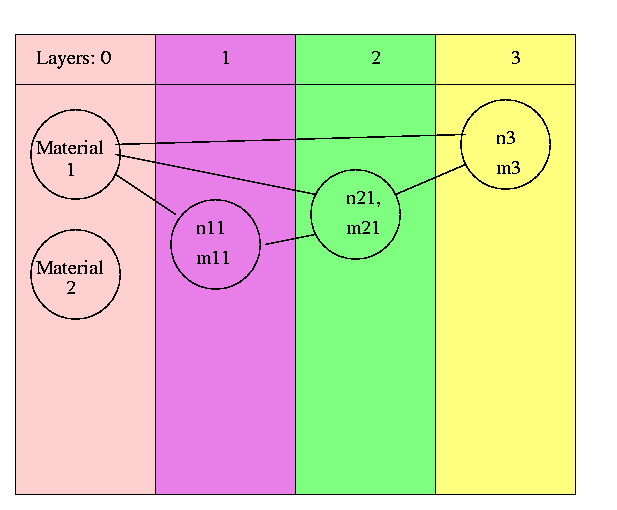 The scheme of assembling
a matrix laminate structure: Material 1 is added to the obtained composite
in differently oriented layers at each step.
The scheme of assembling
a matrix laminate structure: Material 1 is added to the obtained composite
in differently oriented layers at each step.After several steps, we end up with a structure in which the disconnected inclusions of one of the materials is wrapped into another; the first material forms the envelope (matrix), and the second forms the nuclei. (The nuclei can be arbitrary elongated). This structure mimics a composite with inclusions. The effective properties do not depend on the sequence of wrapping; only the relative fractions in the enforced directions are valid.
The symmetric matrix laminates structure has the same properties as the structure of coated spheres,.
An anisotropic matrix laminates structure has the same effective properties as a laminate from the outer material and a matrix laminates made of remaining part of this material with the nucleus from the other one.The effective properties of the structure are given by the formula:
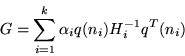
The matrix laminates are known to have:
 Structure of a third rank matrix laminate
Structure of a third rank matrix laminate GO TO THE WORKSHOP