


Next: Effective properties and local
Up: Simple laminates
Previous: Equilibrium
Depending on the constitutive relation, some components of the
fields 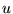 and
and  stays continuous everywhere in a laminate while the
other component are only piece-wise continuous.
stays continuous everywhere in a laminate while the
other component are only piece-wise continuous.
Example
For example, consider conducting materials. The normal component of the
current and the tangent component(s) of the electrical field are
continuous, the remaining components are discontinuous.
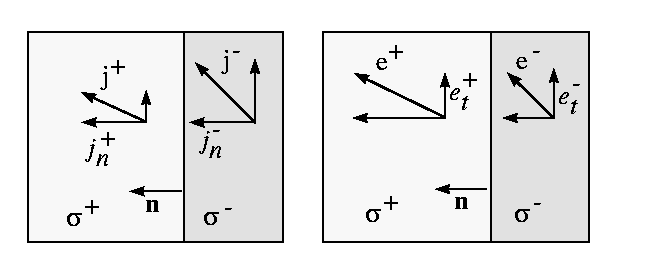
- Generally, the vector field
 is subject to some differential constraints (the vectors may be
divergencefree, curlfree, etc.) These constraints imply that some linear
combinations of its components are continuous on
the boundary between layers,
is subject to some differential constraints (the vectors may be
divergencefree, curlfree, etc.) These constraints imply that some linear
combinations of its components are continuous on
the boundary between layers,
![\begin{displaymath}
{ p} [ { v}_1 -{ v}_2]=0,
\end{displaymath}](img33.gif) |
(3) |
Here  is a matrix projector on the subspace of continuous
components.
is a matrix projector on the subspace of continuous
components.
The components 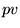 of
of 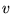 are constant in the
laminate and
the the supplementary orthogonal components
are constant in the
laminate and
the the supplementary orthogonal components 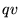 of
of 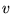 jump on the boundary between layers.
jump on the boundary between layers.
![\begin{displaymath}
{ q} [ { v}_1 -{ v}_2] \neq 0;
\end{displaymath}](img38.gif) |
(4) |
Projections 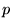 and
and 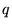 are mutually orthogonal:
are mutually orthogonal:
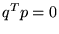
- The dual vector
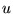 has the properties similar to the vector
has the properties similar to the vector
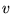 , but its discontinuous components are supplementary to those of
the prime vector
, but its discontinuous components are supplementary to those of
the prime vector 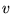 ; in other words, the continuous and
discontinuous components
of
; in other words, the continuous and
discontinuous components
of 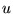 and
and 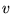 switch their places:
switch their places:
![\begin{displaymath}
{ q} [ { u}_1 -{ u}_2] = 0, \quad { p} [ { u}_1 -{ u}_2] \neq 0.
\end{displaymath}](img42.gif) |
(5) |
The next Table shows discontinuous components 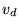 of the fields in
the equations of interest.
These component are completely defined by the normal to the laminate.
The matrix
of the fields in
the equations of interest.
These component are completely defined by the normal to the laminate.
The matrix 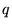 projects vector
projects vector  onto
onto 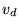 as follows:
as follows:
Table 1:
Space of discontinuous components 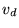 of the fields in various
equilibria
of the fields in various
equilibria
|
Process |
Properties tensor 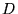 |
Field vector  |
Subspace 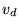 of discontinuous
components
of discontinuous
components |
|
Conductivity |
Conductivity tensor |
Curlfree field |
normal 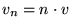 |
|
Conductivity |
Resistivity tensor 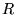 |
Divergencefree current
|
tangent(s)
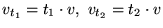 |
|
2D Elasticity |
Stiffness tensor 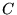 |
Strain 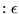
|
the tensorial component
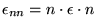
|
|
2D Elasticity |
Compliance tensor 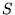 |
Stress 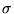 |
two tensorial
components
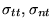 |
|
3D Elasticity |
Stiffness tensor 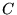 |
Strain 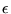 |
Three tensorial
components
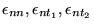
|
|
3D Elasticity |
Compliance tensor 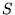 |
Stress 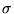 |
Three tensorial
components
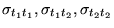 |
|
Maxwell equations |
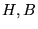 |
. |
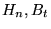 |
|
|
|
|
|



Next: Effective properties and local
Up: Simple laminates
Previous: Equilibrium
Andre Cherkaev
2001-07-31
![]() and
and ![]() stays continuous everywhere in a laminate while the
other component are only piece-wise continuous.
stays continuous everywhere in a laminate while the
other component are only piece-wise continuous.
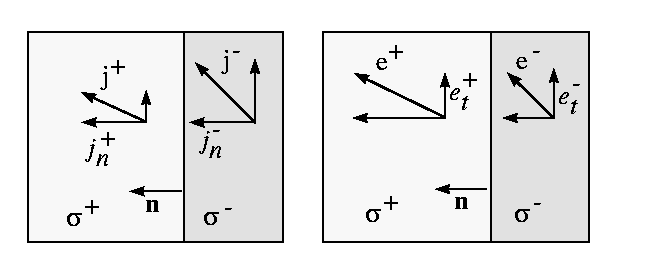
![]() of
of ![]() are constant in the
laminate and
the the supplementary orthogonal components
are constant in the
laminate and
the the supplementary orthogonal components ![]() of
of ![]() jump on the boundary between layers.
jump on the boundary between layers.
![]() of the fields in
the equations of interest.
These component are completely defined by the normal to the laminate.
The matrix
of the fields in
the equations of interest.
These component are completely defined by the normal to the laminate.
The matrix ![]() projects vector
projects vector ![]() onto
onto ![]() as follows:
as follows: