


Next: Continuity of field components
Up: Simple laminates
Previous: Simple laminates
Effective properties of a laminate are defined by the type of
equilibrium in the medium. Here we derive these properties. Assume
that the materials are linear, that is that the constitutive
relation in 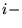 th material is
th material is
Here the vectors 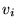 and
and 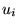 represent the ``prime''
and ``dual'' fields, respectively, joined by the tensor
of material's properties
represent the ``prime''
and ``dual'' fields, respectively, joined by the tensor
of material's properties 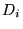 . These fields are constant if the
composite is uniformly loaded or if the width of layers does to zero.
. These fields are constant if the
composite is uniformly loaded or if the width of layers does to zero.
Examples
- For conducting composite,
the constitutive relations is the Ohm's law:
where 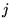 is the current (dual variable),
is the current (dual variable), 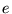 is the electrical field
(prime variable), and
is the electrical field
(prime variable), and
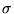 is the conductivity tensor. Of course, we may reverse the
Ohm's law:
is the conductivity tensor. Of course, we may reverse the
Ohm's law:
then 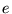 is a dual and
is a dual and 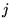 is a prime variable.
is a prime variable.
- For elastic materials, the constitutive relation is the Hook's law
where 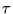 is the symmetric second-rank stress tensor,
is the symmetric second-rank stress tensor, 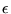 is the
symmetric second-rank strain tensor,
is the
symmetric second-rank strain tensor, 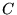 is the fourth-rank tensor of elastic
stiffness, (:) is the scalar product in the tensor space.
is the fourth-rank tensor of elastic
stiffness, (:) is the scalar product in the tensor space.
Let us derive the effective properties of
a two-component laminate. It is characterized by a normal 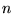 and by volume fractions
and by volume fractions 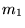 and
and 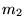 of subdomains
of subdomains
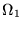 and
and
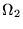 that are occupied
by the materials with tensor properties
that are occupied
by the materials with tensor properties 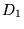 and
and 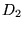 .
The composite
is submerged into a uniform field
.
The composite
is submerged into a uniform field 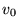 .
.
The fields 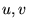 in the laminates are
piecewise constant:
in the laminates are
piecewise constant:
where 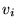 = constant(
= constant(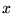 ).
).
The effective tensor of laminate
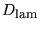 joins the averaged fields
joins the averaged fields
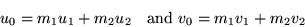 |
(1) |
as follows:
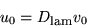 |
(2) |
where
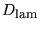 is the effective tensor of
laminates which we are determining here.
is the effective tensor of
laminates which we are determining here.



Next: Continuity of field components
Up: Simple laminates
Previous: Simple laminates
Andre Cherkaev
2001-07-31
![]() and by volume fractions
and by volume fractions ![]() and
and ![]() of subdomains
of subdomains
![]() and
and
![]() that are occupied
by the materials with tensor properties
that are occupied
by the materials with tensor properties ![]() and
and ![]() .
The composite
is submerged into a uniform field
.
The composite
is submerged into a uniform field ![]() .
.
![]() in the laminates are
piecewise constant:
in the laminates are
piecewise constant:
![]() joins the averaged fields
joins the averaged fields